Chứng minh rằng M nằm ngoài đường tròn đường kính AB <=> góc AMB < 90o

Những câu hỏi liên quan
Cho đường tròn tâm O bán kính 5cm điểm M nằm ngoài đường tròn kẻ các tiếp tuyến MA,MB với đường tròn ,biết góc AMB=60° a, chứng minh MA=MB b, chứng minh ∆AMB là ∆ đều
a: Xét (O) có
MA,MB là tiếp tuyến
nên MA=MB
b: Xét ΔMAB có MA=MB và góc AMB=60 độ
nên ΔMAB đều
Đúng 0
Bình luận (0)
Chứng minh rằng M nằm trong đường tròn đường kính AB <=> góc AMB > 90o
(=>)
M nằm trong đường tròn, Kéo dài AM cắt đtr đk AB tại C
Tam giác ACB nội tiếp đường trong đường kính AB => góc ACB = 90o
Mà góc AMB là góc ngoài của tam giác BCM tại đỉnh M nên góc AMB > góc ACB => góc AMB > 90o
(<=) Chứng minh phản chứng:
Giả sử M ngoài đtr đk AB
Gọi C là giao của AM với đtr => tam giác ACB vuông tại C => góc ACB = 90o
Ta có: góc ACB là góc ngoài của tam giác BMC tại đỉnh C => góc ACB > BMC => 90o > AMB (trái với giả thiết)
Vậy điều giả sử sai
=> đpcm
Đúng 0
Bình luận (0)
Cho đường tròn o , điểm M nằm ngoài đường tròn . kẻ các tiếp tuyến MA,MB với đường tròn (B,C là các tiếp điểm) a,Chứng minh ∆AMB cân b,Cho góc AMB=60°.Tính gócAOB c,Chứng minh MO vuông góc AB
a: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>ΔMAB cân tại M
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}+\widehat{AMB}+\widehat{AOB}=360^0\)
=>\(\widehat{AOB}+60^0+90^0+90^0=360^0\)
=>\(\widehat{AOB}+240^0=360^0\)
=>\(\widehat{AOB}=120^0\)
c: ta có: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB
Đúng 1
Bình luận (0)
Từ điểm M nằm ngoài đường tròn (O;R) vẽ hai tiếp tuyến MA, MB đến đường tròn ( A, B là tiếp điểm). AB cắt OM tại H. a) Chứng minh rằng: AB vuông góc với OM. b) Chứng minh rằng: HO.HM = 4 2 AB c) Kẻ đường kính AD. Từ O kẻ OI vuông góc với MD ( I MD ), OI cắt AB tại E. Chứng minh rằng: ED là tiếp tuyến của đường đường tròn (O)
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
hay OM⊥AB
Đúng 0
Bình luận (0)
Từ điểm M nằm ngoài đường tròn (O;R) vẽ hai tiếp tuyến MA, MB đến đường tròn ( A, B là tiếp điểm). AB cắt OM tại H. a) Chứng minh rằng: AB vuông góc với OM. b) Chứng minh rằng: HO.HM = 4 2 AB c) Kẻ đường kính AD. Từ O kẻ OI vuông góc với MD ( I MD ), OI cắt AB tại E. Chứng minh rằng: ED là tiếp tuyến của đường đường tròn (O)
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
b: Xét ΔOAM vuông tại A có AH là đường cao
nên \(HO\cdot HM=HA^2\)
=>\(HO\cdot HM=\left(\dfrac{1}{2}AB\right)^2=\dfrac{1}{4}AB^2\)
c: Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2=OD^2\left(3\right)\)
Xét ΔOIM vuông tại I và ΔOHE vuông tại H có
\(\widehat{HOE}\) chung
Do đó: ΔOIM đồng dạng với ΔOHE
=>\(\dfrac{OI}{OH}=\dfrac{OM}{OE}\)
=>\(OI\cdot OE=OH\cdot OM\left(4\right)\)
Từ (3) và (4) suy ra \(OI\cdot OE=OD^2\)
=>\(\dfrac{OI}{OD}=\dfrac{OD}{OE}\)
Xét ΔOID và ΔODE có
\(\dfrac{OI}{OD}=\dfrac{OD}{OE}\)
\(\widehat{DOE}\) chung
DO đó: ΔOID đồng dạng với ΔODE
=>\(\widehat{OID}=\widehat{ODE}=90^0\)
=>ED là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Bài1 : Cho đường tròn (O,5cm) điểm M nằm bên ngoài đường tròn. Kể các tiếp tuyến MA, MB với đường tròn ( AB là tiếp điểm) biết góc AMB 60 độa: Chứng minh AMB là tam giác đềub: Tính chu vi tam giác AMBc: Tia AO cắt đường tròn ở C; tứ giác BMOC là hình gì? Vì sao?Bài 2 : Cho đường tròn (O) đường kính AB, gọi M là một điểm tùy ý trên đường tròn, xy là tiếp tuyến của đường tròn tại A, qua M kẻ MP vuông góc AB, MQ vuông góc xya: tứ giác APMQ là hình gì? Vì sao?b: gọi I là trung điểm PQ. Chứn...
Đọc tiếp
Bài1 : Cho đường tròn (O,5cm) điểm M nằm bên ngoài đường tròn. Kể các tiếp tuyến MA, MB với đường tròn ( AB là tiếp điểm) biết góc AMB= 60 độ
a: Chứng minh AMB là tam giác đều
b: Tính chu vi tam giác AMB
c: Tia AO cắt đường tròn ở C; tứ giác BMOC là hình gì? Vì sao?
Bài 2 : Cho đường tròn (O) đường kính AB, gọi M là một điểm tùy ý trên đường tròn, xy là tiếp tuyến của đường tròn tại A, qua M kẻ MP vuông góc AB, MQ vuông góc xy
a: tứ giác APMQ là hình gì? Vì sao?
b: gọi I là trung điểm PQ. Chứng minh OI vuông góc AM
Bài 1:
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay ΔMAB cân tại M
mà \(\widehat{AMB}=60^0\)
nên ΔMBA đều
b: Xét ΔAOM vuông tại A có
\(AM=OA\cdot\tan30^0\)
nên \(AM=5\sqrt{3}\left(cm\right)\)
\(C_{AMB}=3\cdot AM=15\sqrt{3}\left(cm\right)\)
c: Ta có: MA=MB
nên M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
hay MO⊥AB(1)
Xét (O) có
ΔABC nội tiếp
AC là đường kính
DO đó: ΔABC vuông tại B
Suy ra: AB⊥BC(2)
Từ (1) và (2) suy ra OM//BC
hay BMOC là hình thang
Đúng 0
Bình luận (0)
Bài1 : Cho đường tròn (O,5cm) điểm M nằm bên ngoài đường tròn. Kể các tiếp tuyến MA, MB với đường tròn ( AB là tiếp điểm) biết góc AMB 60 độa: Chứng minh AMB là tam giác đềub: Tính chu vi tam giác AMBc: Tia AO cắt đường tròn ở C; tứ giác BMOC là hình gì? Vì sao?Bài 2 : Cho đường tròn (O) đường kính AB, gọi M là một điểm tùy ý trên đường tròn, xy là tiếp tuyến của đường tròn tại A, qua M kẻ MP vuông góc AB, MQ vuông góc xya: tứ giác APMQ là hình gì? Vì sao?b: gọi I là trung điểm PQ. Chứng minh OI...
Đọc tiếp
Bài1 : Cho đường tròn (O,5cm) điểm M nằm bên ngoài đường tròn. Kể các tiếp tuyến MA, MB với đường tròn ( AB là tiếp điểm) biết góc AMB= 60 độ
a: Chứng minh AMB là tam giác đều
b: Tính chu vi tam giác AMB
c: Tia AO cắt đường tròn ở C; tứ giác BMOC là hình gì? Vì sao?
Bài 2 : Cho đường tròn (O) đường kính AB, gọi M là một điểm tùy ý trên đường tròn, xy là tiếp tuyến của đường tròn tại A, qua M kẻ MP vuông góc AB, MQ vuông góc xy
a: tứ giác APMQ là hình gì? Vì sao?
b: gọi I là trung điểm PQ. Chứng minh OI vuông góc AM
c
Gọi H là giao điểm của AB và OM
a, Xét Δv MAO và ΔvMBO
Có MO chung
AO=OB(=bk)
=> ΔvMAO= ΔMBO (ch-cgv)
=> MA=MB
Trong ΔAMB
Có MA=MB(cmt)
=> ΔAMB cân tại M
lại có góc AMB=60 độ
=> ΔAMB là Δ đều
b, Ta có: góc AMO=góc BMO ( ΔvMAO= ΔvMBO)
mà góc AMO+ góc BMO= góc AMB=60 độ
=> góc AMO=\(\frac{1}{2}.60=30^0\)
Áp dụng tỉ số lượng giác
Ta có : tan góc AMO=\(\frac{AO}{AM}\)
tan30=\(\frac{5}{AM}\)
=>AM=\(\frac{5}{tan30}=5\sqrt{3}\)
Chu vi ΔAMB= AM.3=\(5\sqrt{3}.3=15\sqrt{3}\)
c, Ta có OA=OB (=bk)
=> O thuộc đường trung trực AB(1)
MA=MB(cmt)
=> M thuộc đường trung trực AB (2)
Từ (1)(2)=> OM là cả đường trung trực
=> MO vuông góc AB (*)
Ta có: OA=OB=OC(=bk)
=> OB=\(\frac{1}{2}AC\)
mà OB là đường trung tuyến
=> Δ ABC vuông tại B
=> AB vuông góc BC(**)
Từ (*)(**)=> MO//BC
=> BMOC là hình thang
Đúng 0
Bình luận (1)
Bài 2:
a,
Ta có : góc AQM=90 độ ( MQ vuông góc xy)
góc APM =90 độ ( MP vuông góc AB)
góc QAP=90độ ( xy vuông góc OA)
=> QMPA là hình chữ nhật
b, Trong hình chữ nhật QMPA:
Có : I là trung điểm của đường chéo thứ nhất QP
-> I cũng là trung điểm của đường chéo thứ 2 AM
=> IA=IM
=> OI vuông góc AM tại I ( đường kính đi qua trung điểm => vuông góc ( đ/Lý 3)
Đúng 0
Bình luận (1)
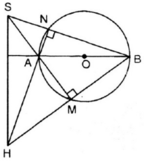
Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.
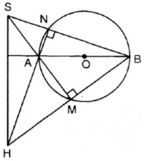
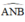 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 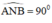 ⇒ AN ⊥ NB
⇒ AN ⊥ NB
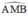 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 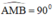 ⇒ AM ⊥ MB
⇒ AM ⊥ MB
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)
Kiến thức áp dụng
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Trong một tam giác, ba đường cao đồng quy tại trực tâm.
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.
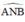 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 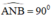 ⇒ AN ⊥ NB
⇒ AN ⊥ NB
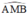 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 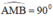 ⇒ AM ⊥ MB
⇒ AM ⊥ MB
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)
Đúng 0
Bình luận (0)












