Nhờ các bạn giúp mình với ạ, mình cần gấp để thi HKII....thank you
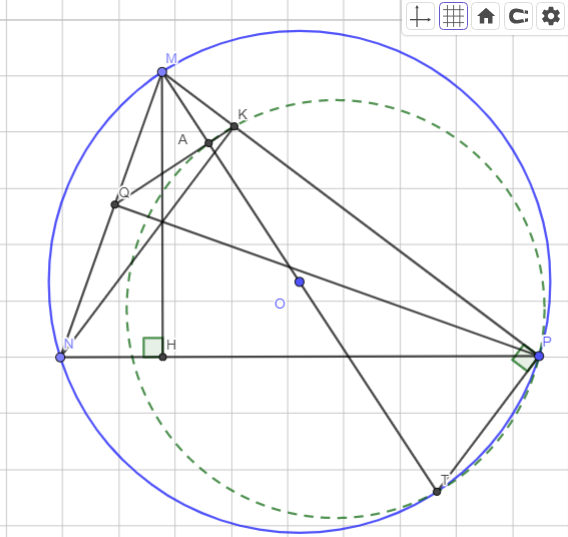
Cho tam giác nhọn DEF ( DE<DF<EF) M là trung điểm của EF, kẻ EN và FP vuông góc với DM( N,P thuộc DM0
a) so sánh các góc của tam giác DEF
b) c/m tam giác ENM = tam giác FPM
c)c/m EP//FN
d) gọi Q là trung điểm của EP,R là trung điểm FP, I là giao điểm NQ và EM, K là giao điểm của NR và FM. c/m EI=IK=KF.