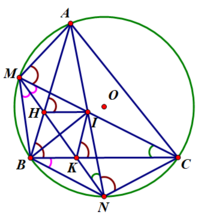
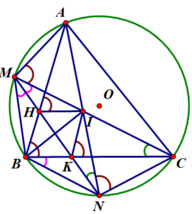
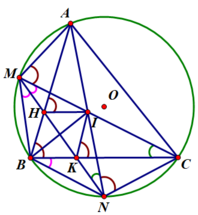
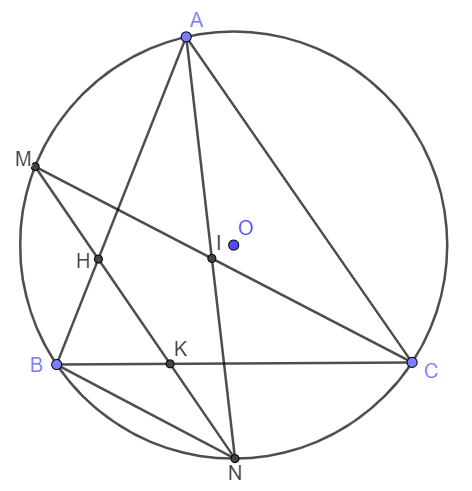
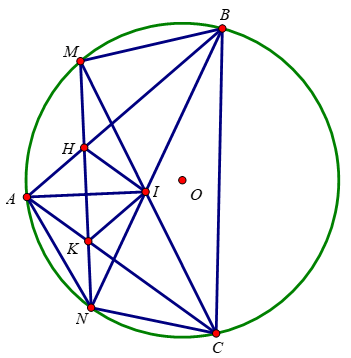
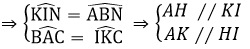Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại I. Dây MN cắt cạnh AB và BC lần lượt tại H và K
a, Chúng minh bốn điểm C, N, K, I cùng thuộc một đường tròn
b, Chứng minh \(NB^2\)=NK\(\times\)NM
c, chứng minh tứ giác BHIK là hình thoi
d, Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của PQ. Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng