cho hình chóp S.ABCD có đáy ABCD là hình vuông bằng a. SA vuông góc (ABCD) và SA bằng a√3. khi đó giữa hai mặt phẳng (SBC) và (ABCD) có số đo bằng
A.60 độ b. 90độ C. 30 ĐỘ D.45độ
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc mặt phẳng ABCD và SA = a góc giữa đường thẳng SB và mặt phẳng ABCD bằng: A 45 độ B 90 độ C 30 độ D 60 độ
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a 6 , B A D ^ = 60 ° , cạnh bên SA vuông góc với đáy và SA = 3a. Số đo của góc giữa hai mặt phẳng (SBC) và (SCD) bằng
A. 90 °
B. 60 °
C. 30 °
D. 45 °
Hình chóp S.ABCD có đáy là hình thoi cạnh a, góc B A C = 60 o , SA vuông góc với mp(ABCD) góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 60 ° . Khoảng cách từ A đến mp (SBC) bằng:
A. a 2 3
B. 2a
C. 3 a 4
D. a
Đáp án C

Gọi E và H lần lượt là hình chiếu của A lên CB và SE
Ta có: A E = A B sin A B E ^ = s i n 60 ° = a 3 2
A H = A E sin 60 ° = 3 2 a . 3 2 = 3 a 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBC) và mặt phẳng đáy bằng 60 ° . Khoảng cách từ D đến mặt phẳng (SBC) bằng
A. 6 a 4
B. a 2
C. 3 a 2
D. 15 a 3
cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, SA vuông góc với mặt phẳng đáy, SA=BD=a√3. Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) bằng
A. 60° B. 30° C.90° D.45°
Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ∠ B A D = 60 0 , cạnh bên SA vuông góc với đáy. Biết rằng góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 Độ dài đoạn thẳng SA bằng
A. a 6 4
B. a 6 2
C. a 3 2
D. a 3 4
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 0 , cạnh bên SA vuông góc với đáy. Biết rằng góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 . Độ dài đoạn thẳng SA bằng
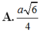
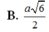
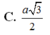
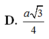
Cho hình chóp S.ABCD có có đáy là hình thoi cạnh a, góc ABC = 120 độ, SA vuông góc với (ABCD). Biết góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 độ. K là trung điểm của SC tính d(BK;AD)
Dễ dàng chứng minh \(BD\perp\left(SAC\right)\Rightarrow BD\perp SC\)
Gọi O là tâm đáy, kẻ \(OH\perp SC\Rightarrow SC\perp\left(BDH\right)\)
\(\Rightarrow\widehat{BHD}\) hoặc góc bù của nó là góc giữa (SBC) và (SCD) \(\Rightarrow\widehat{BHD}=60^0\) hoặc \(120^0\)
\(\Rightarrow\widehat{BHO}\) bằng \(30^0\) hoặc \(60^0\)
Tam giác ABD đều \(\Rightarrow BD=a\) \(\Rightarrow OB=\dfrac{a}{2}\)
TH1: \(\widehat{BHO}=30^0\)
\(\Rightarrow OH=\dfrac{OB}{tan30^0}=\dfrac{a\sqrt{3}}{2}=OC\Rightarrow\Delta\) vuông OCH có cạnh huyền bằng cạnh góc vuông (loại)
TH2: \(\widehat{BHO}=60^0\Rightarrow OH=\dfrac{OB}{tan60^0}=\dfrac{a\sqrt{3}}{6}\)
\(\Rightarrow SA=AC.tan\widehat{SCA}=AC.\dfrac{OH}{\sqrt{OC^2-OH^2}}=\dfrac{a\sqrt{6}}{4}\)
Từ A kẻ \(AM\perp SB\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM=d\left(A;\left(SBC\right)\right)\)
\(AD||BC\Rightarrow AD||\left(SBC\right)\Rightarrow d\left(BK;AD\right)=d\left(AD;\left(SBC\right)\right)=d\left(A;\left(SBC\right)\right)=AM\)
\(\dfrac{1}{AM^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{11}{3a^2}\Rightarrow AM=\dfrac{a\sqrt{33}}{11}\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD).
a) Chứng minh BD ⊥ SC.
b) Chứng minh (SAB) ⊥ (SBC).
c) Cho SA = (a√6)/3. Tính góc giữa SC và mặt phẳng (ABCD).
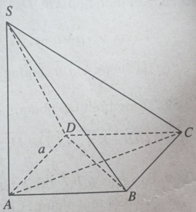
a) (BD ⊥ SA & BD ⊥ AC ⇒ BD ⊥ (SAC)
⇒ BC ⊥ SC.
b) (BC ⊥ SA & BC ⊥ AB ⇒ BC ⊥ (SAB)
⇒ (SBC) ⊥ (SAB).
c) + Xác định góc α giữa đường thẳng SC và mp(ABCD):
(C ∈(ABCD) & SA ⊥ (ABCD) ⇒ ∠[(SC,(ABCD))] = ∠(ACS) = α
+ Tính góc:
Tam tam giác vuông SCA, ta có:
tanα = SA/AC = √3/3 ⇒ α = 30 o .
Cho hình chóp S. ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng a 2 và SA vuông góc với mặt phẳng (ABCD). Gọi α là góc giữa hai mặt phẳng (SBD) và (ABCD). Nếu tan α = 2 thì góc giữa hai mặt phẳng (SAC) và (SBC) bằng:
A. 300
B. 600
C. 450
D. 900
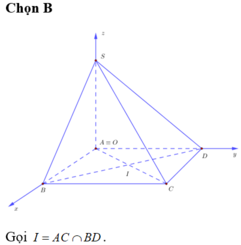
Hình vuông ABCD có độ dài đường chéo bằng a√2 suy ra hình vuông đó có cạnh bằng a.
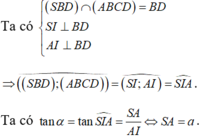
Chọn hệ trục tọa độ Oxyz như hình vẽ. Ta có A (0;0;0), B (a;0;0), C (a;a;0), S (0;0;a).
