Ví dụ 4: Cho tam giác ABE vuông tại E, đường cao EH. Cho AE = 6cm, BE.Tinh ĐH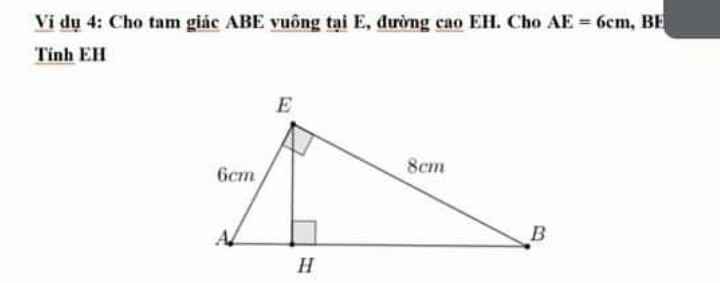

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có đường phân giác của góc ABC cắt AC tại E . Kẻ EH vuông góc với BC tại H ( H thuộc BC ) chứng minh a ) tam giác ABE =tam giác HBE b) HEC= 2ABE c) EC >AE
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔABE=ΔHBE
b: góc HEC+góc AEH=180 độ
góc AEH+góc ABH=180 độ
=>góc HEC=góc ABH=2*góc ABE
c: AE=EH
EH<EC
=>AE<EC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,đường phân giác BE(E thuộc AC)Kẻ EH vuông góc BC(H thuộc BC)
a)Tính góc BAC
b)Chứng minh góc ABE=góc CBE và tam giác ABE=tam giác HBE
c)Chứng minh BE là đường trung trực của AH
d)Kẻ đường cao AK của tam giác ABC.Chứng minh AB+AC<BC+2AK
e)Tia HE cắt tia BA tại M.Chứng minh BE vuông góc MC
Giúp mình với mọi người
cho tam giác ABC vuông tại A có AB=6cm, AC=8cm
a) tính độ dài BC?
b) trên tia BA lấy điểm D sao cho BD=BC. Nối D và C, vẽ đường cao DE của tam giác BDC (E thuộc BC). chứng minh tam giác BAC=tam giác BED
c) chứng minh tam giác ABE cân và AE song song DC
d) gọi M là trung điểm của AC. Hai đường thẳng AE và DM cắt nhau tại H. chứng minh tam giác ACH vuông
bài 4: cho tam giác ABC vuông tại A có đường phân giác của góc ABC cắt AC tại E . Kẻ EH vuông góc BC tại H (H thuộc BC) Chứng minh a) tam giác ABE= tam giác HBE b) BE là đường trung trực của đoạn thẳng AH c) EC>AE
cho tam giác ABC vuông tại A đường cao AH a, đường phân giác góc ABC cắt AC tại D,DH tại E chứng minh AD nhân AE =DC nhân EH
Cho tam giác ABC vuông tại A có đường phân giác của góc ABC cắt AC tại E.
kẻ EH vuông góc với BC tại H (H thuộc BC ). chứng minh :
a) tam giác ABE = tam giác HBE
b) BE là đường trung trực của đoạn thẳng AH
c) EC > AE
Cho tam giác ABC vuông tại A có đường phân giác của góc ABC cắt AC tại E.Kẻ EH vuông góc với BC tại H(H thuộc BC).Chứng minh a)tam giác ABE bằng tam giác HBE b)HEC=2ABE c)EC>AE
a) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)
Đúng 1
Bình luận (0)
cho tam giác ABC có A=90 độ, BE là đường phân giác của B cắt cạnh AC tại E (E thuộc AC) kẻ EH vuông góc với BC (H thuộc BC)
a) chứng minh tam giác ABE=tam giác HBE và AE=EH
b)chứng minh BE là đường trung trực của AH
c)chung minh AE<EC
cho tam giác ABC vuông tại A có đường phân giác BE {E thuộc AC}. kẻ EH vuông BC
+ TÍNH góc BAC
+ góc ABE = góc CBE
+Chúng minh BE là đường trung trực của AH
+Gọi AK là đường cao của tam giác ABC
chứng minh AB+AC< BC+AK

















