Ta có:

\(\left(x^2+1\right)^2+3x\left(x^2+1\right)+2x^2=0\)

\(\Leftrightarrow x^4+2x^2+1+3x^3+3x+2x^2=0\)

\(\Leftrightarrow x^4+3x^3+4x^2+3x+1=0\)

Xét x = 0 không là nghiệm của pt

Chia 2 vế của pt cho x² ta được:

\(x^2+3x+4+\dfrac{3}{x}+\dfrac{1}{x^2}=0\)

\(\Leftrightarrow\left(x^2+\dfrac{1}{x^2}\right)+\left(3x+\dfrac{3}{x}\right)+4=0\)

\(\Leftrightarrow\left(x^2+\dfrac{1}{x^2}\right)+3\left(x+\dfrac{1}{x}\right)+4=0\)

Đặt a = \(x+\dfrac{1}{x}\)

\(\Leftrightarrow x^2+2+\dfrac{1}{x^2}=a^2\)

\(\Leftrightarrow x^2+\dfrac{1}{x^2}=a^2-2\)

Suy ra:

\(\Leftrightarrow\left(a^2-2\right)+3a+4=0\)

\(\Leftrightarrow a^2+3a+2=0\)

\(\Leftrightarrow\left(a+1\right)\left(a+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=-1\\a=-2\end{matrix}\right.\)

Với a = -1

=> \(x+\dfrac{1}{x}=-1\)

\(\Rightarrow x^2+1=-x\) (loại)

Với a = -2

=> \(x+\dfrac{1}{x}=-2\)

\(\Rightarrow x^2+1+2x=0\)

\(\Leftrightarrow\left(x+1\right)^2=0\)

\(\Leftrightarrow x=-1\)

Vây pt có tập nghiệm là: \(S=\left\{-1\right\}\)

Ta có:\(2a^2+2b^2=5ab\)

\(\Leftrightarrow2a^2-5ab+2b^2=0\)

\(\Leftrightarrow2a^2-ab-4ab+2b^2=0\)

\(\Leftrightarrow a\left(2a-b\right)-2b\left(2a-b\right)=0\)

\(\Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a-2b=0\left(loai\right)\\2a-b=0\end{matrix}\right.\Leftrightarrow2a=b\)

\(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{a+2a}{a-2a}=-3\)

1)Cách khác:

\(\left(x^2+1\right)^2+3x\left(x^2+1\right)+2x^2=0\)

\(\Leftrightarrow\left(x^2+1\right)^2+x\left(x^2+1\right)+2x\left(x^2+1\right)+2x^2=0\)

\(\Leftrightarrow\left(x^2+1\right)\left(x^2+x+1\right)+2x\left(x^2+1+x\right)=0\)

\(\Leftrightarrow\left(x^2+x+1\right)\left(x^2+2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+x+1=0\left(loai\right)\\x^2+2x+1=0\end{matrix}\right.\)

\(\Leftrightarrow x=-1\)

b, \(\frac{a^3}{b+2c}+\frac{b^3}{c+2a}+\frac{c^3}{a+2b}\ge1\)

\(\frac{a^4}{ab+2ac}+\frac{b^4}{bc+2ab}+\frac{c^4}{ac+2bc}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac+2ac+2ab+2bc}\)( Bunhia dạng phân thức )

mà \(a^2+b^2+c^2\ge ab+bc+ac\)

\(=\frac{\left(ab+bc+ac\right)^2}{3+2\left(ab+ac+bc\right)}=\frac{9}{3+6}=1\)( đpcm ) 

1.

Điều kiện x \ge \dfrac14x≥41​.

Phương trình tương đương với \left(\sqrt2.\sqrt{2x^2+x+1}-2\right)-\left(\sqrt{4x-1}-1\right)+2x^2+3x-2 = 0(2​.2x2+x+1​−2)−(4x−1​−1)+2x2+3x−2=0 \Leftrightarrow \dfrac{4x^2+2x-2}{\sqrt2.\sqrt{2x^2+x+1}+2} - \dfrac{4x-2}{\sqrt{4x-1}+1} + (x+2)(2x-1) = 0⇔2​.2x2+x+1​+24x2+2x−2​−4x−1​+14x−2​+(x+2)(2x−1)=0\\ \Leftrightarrow (2x-1)\left(\dfrac{2(x+1)}{\sqrt2 \sqrt{2x^2+x+1}+2} - \dfrac2{\sqrt{4x-1}+1} + x + 2\right) = 0⇔(2x−1)(2​2x2+x+1​+22(x+1)​−4x−1​+12​+x+2)=0

\Leftrightarrow \left[\begin{aligned} & x =\dfrac12\\ & \dfrac{2(x+1)}{\sqrt2 \sqrt{2x^2+x+1}+2} - \dfrac2{\sqrt{4x-1}+1} + x + 2 = 0\\ \end{aligned}\right.⇔⎣⎢⎢⎢⎡​​x=21​2​2x2+x+1​+22(x+1)​−4x−1​+12​+x+2=0​

Với x \ge \dfrac14x≥41​ ta có:

\dfrac{2(x+1)}{\sqrt2 \sqrt{2x^2+x+1}+2} > 02​2x2+x+1​+22(x+1)​>0

- \dfrac2{\sqrt{4x-1}+1} \ge -2−4x−1​+12​≥−2

$x+2>2$.

Suy ra \dfrac{2(x+1)}{\sqrt2 \sqrt{2x^2+x+1}+2} - \dfrac2{\sqrt{4x-1}+1} + x + 2 > 02​2x2+x+1​+22(x+1)​−4x−1​+12​+x+2>0.

Vậy phương trình có nghiệm duy nhất x = \dfrac12.x=21​.

2.

Đặt P = \dfrac{a^3}{b+2c} + \dfrac{b^3}{c+2a} + \dfrac{c^3}{a+2b}P=b+2ca3​+c+2ab3​+a+2bc3​

Áp dụng bất đẳng thức Cauchy cho hai số dương \dfrac{9a^3}{b + 2c}b+2c9a3​ và $(b+2c)a$ ta có

\dfrac{9a^3}{b+2c} + (b+2c)a \ge 6a^2b+2c9a3​+(b+2c)a≥6a2.

Tương tự \dfrac{9b^3}{c+2a} + (c+2a)b \ge 6b^2c+2a9b3​+(c+2a)b≥6b2, \dfrac{9c^3}{a+2b} + (a+2b)c \ge 6c^2a+2b9c3​+(a+2b)c≥6c2.

Cộng các vế ta có 9P + 3(ab+bc+ca) \ge 6(a^2+b^2+c^2)9P+3(ab+bc+ca)≥6(a2+b2+c2).

Mà a^2+b^2+c^2 \ge ab+bc+ca = 4a2+b2+c2≥ab+bc+ca=4 nên $P\ge 1$ (ta có đpcm).

1.

√2 × √(2x²+x+1)        +      √(4x-1) + 3x-3=0

⇌[√(4x²+2x+2)-2] - [√(4x-1)     -1] + (2x²+3x-2)=0

⇌(4x²+2x-2)/[√(4x²+2x+2)+2] - (4x-2)/[√(4x-1)+1] + (2x-1)(x+2) =0

⇔(2x-1) × [(2x+2)/√(4x²+2x+2+2) - 2/(√4x-1)+1+x+2]=0

Với x≥1/4 thì (2x+2)/(√4x²+2x+2+2)≥0 hoặc x+2>2 hoặc (√4x-1)+1≥1 ⇌ 2/[(√4x-1)+1]≤2

⇒(2x+2)/[(√4x²+2x+2)+2] - 2/[(x-1)+1]+x+2>0-2+2=0

⇌ 2x-1=0⇒x=1/2 

Vậy x=1/2

2.

Áp dụng bất đẳng thức ta có :

Vế trái = a⁴/(ab +2ac)    +   b⁴/(bc+2ab)  + c⁴/(ac+2bc)≥[(a² + b² +c²)²]/[3(ab+bc+ca) =[(a²+b²+c²)²]/9

Ấp dụng bất đẳng thức ta có :

ab+bc+ca≤a²+b²+c² 

Vế trái ≥ [(a²+b²+c²)]/9≥3²/9 =1

⇒ Vế trái ≥1 (đpcm)

Dấu = xảy ra khi a=b=c=1

2, (trích đề thi học sinh giỏi Bến Tre-1993)

\(a^3+a^2b+ca^2+b^3+ab^2+b^2c+c^3+c^2b+c^2a=a^2\left(a+b+c\right)+b^2\left(a+b+c\right)+c^2\left(a+b+c\right)=\left(a+b+c\right)\left(a^2+b^2+c^2\right)\)

mà a+b+c=0 => (a+b+c)(a²+b²+c²)=0 

=> đpcm

*bài này tui làm tắt, không hiểu ib 

Vừa lm xog bị troll chứ, tuk quá 

\(x-a^2x-\frac{b^2}{b^2-x^2}+a=\frac{x^2}{x^2-b^2}\)

\(\Leftrightarrow\frac{x\left(b^2-x^2\right)\left(x^2-b^2\right)}{\left(b^2-x^2\right)\left(x^2-b^2\right)}-\frac{a^2x\left(b^2-x^2\right)\left(x^2-b^2\right)}{\left(b^2-x^2\right)\left(x^2-b^2\right)}-\frac{b^2\left(x^2-b^2\right)}{\left(b^2-x^2\right)\left(x^2-b^2\right)}+\frac{a\left(b^2-x^2\right)\left(x^2-b^2\right)}{\left(b^2-x^2\right)\left(x^2-b^2\right)}=\frac{x^2\left(b^2-x^2\right)}{\left(b^2-x^2\right)\left(x^2-b^2\right)}\)

Khử mẫu : 

\(\Leftrightarrow2x^3b^2-xb^4-x^5-2a^2x^3b^2+a^2xb^4+a^2x^5-b^2x^2+b^4+2ab^2x^2-ab^4-ax^4=x^2b^2-x^4\)

Tự xử nốt, lm bài này muốn phát điên mất. 

đk \(x\ne\pm b\)

quy đồng mẫu, khử mẫu chung, ta đưa phương trình đã cho về phương trình

\(\left(x^2-b^2\right)\left[\left(1-a\right)-\left(1-a^2\right)x\right]=0\)(1)

với điều kiện x²-b² khác 0, phương trình (1)trở thành (1-a)-(1-a²)x=0  <=> (1-a²)x=1-a (2)

với a=\(\pm\)1 => (2) vô ngiệm => (1) cũng vô nghiệm và phương trình đã cho cũng vô nghiệm

với a khác \(\pm\)1 => (2) có nghiệm \(x=\frac{1}{1+a}\)

để giá trị x=\(\frac{1}{1+a}\)là nghiệm của phương trình đã cho thì \(\frac{1}{1+a}\ne\pm b\)

kết quả: a=\(\pm1\Rightarrow S=\varnothing\)

\(\hept{\begin{cases}a\ne\pm1\\\frac{1}{1+a}\ne\pm b\end{cases}\Rightarrow S=\left\{\frac{1}{1+a}\right\}}\)

 Tập nghiệm của bất phương trình đã cho là đoạn [2a - b + 1; -a + 2b - 1] (nếu 2a - 6 + 1 ≤ -a + 26 - 1) hoặc là đoạn [-a + 26 - 1 ; 2a - 6 + 1] (nếu -a + 2b - 1 ≤ 2a - 6 - 1)

    Do đó để tập nghiệm của bất phương trình đã cho là đoạn [0;2], điều kiện cần và đủ là:

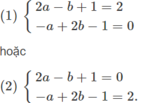
Giải (1) ta được a = b = 1. Giải hệ (2) ta được a = 1/3, b = 5/3

    Đáp số: a = b = 1 hoặc a = 1/3, b = 5/3

1:

a: 2x-3=5

=>2x=8

=>x=4

b: (x+2)(3x-15)=0

=>(x-5)(x+2)=0

=>x=5 hoặc x=-2

2:

b: 3x-4<5x-6

=>-2x<-2

=>x>1

Sửa lại đề bài:  1 / 2a- b 

                   ( MÁY MK KO ĐÁNH ĐC PHÂN SỐ MONG BN THÔNG CẢM)

mới lm đc nhé bn! 

a) ĐKXĐ: bn tự lm nhé ! 

bn biến đổi: 2a³-b+2a-a²b =  (2a-b)  + ( 2a³-a²b) = (2a-b) + a²(2a-b) = (2a-b)(a²+1) 

rồi bn nhân 1 / 2a+b với a²+1 rồi trừ 2 phân thức với nhau sẽ ra 0 => A=0

Bạn nào giúp tớ với!

ai giúp tui không?!!