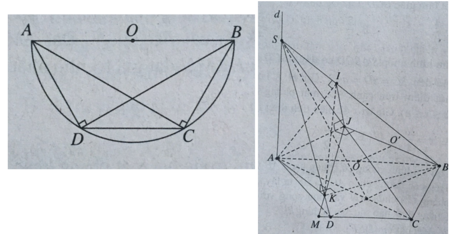
Nhận xét

Hình thang ABCD có hai cạnh bên và đáy nhỏ bằng nhau và bằng nửa đáy lớn, nên nó là nửa lục giác đều nội tiếp trong đường tròn đường kính AB, tâm O là trung điểm của AB.

Như vậy: ∠(ACB) = ∠(ADB) = 1v.

a) Theo giả thiết, ta có: SA ⊥ (ABCD) ⇒ SA ⊥ BC

BC ⊥ SA & BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC. (1)

Mặt khác SB ⊥ (P) nên SB ⊥ IJ (⊂ (P)) (2)

Từ (1) và (2) suy ra BCJI là tứ giác nội tiếp trong đường tròn đường kính BJ.

Ta có BC ⊥ (SAC) ⇒ BC ⊥ AJ (⊂ (SAC))

AJ ⊥ BC & AJ ⊥ SB (do SB ⊥ (P)) ⇒ AJ ⊥ (SBC) ⇒ AJ ⊥ JI (⊂ (SBC)) (3)

Lý luận tương tự, ta có:

BD ⊥ AD & BD ⊥ SA ⇒ BD ⊥ (SAD) ⇒ BD ⊥ AK (⊂ (SAD))

AK ⊥ BD & AK ⊥ SB(⊂ (P)) ⇒ AK ⊥ (SBD) ⇒ AK ⊥ KI. (4)

Từ (3) và (4) suy ra AKJI nội tiếp trong đường tròn đường kính AI nằm trong mặt phẳng (P).

b) Ta có ngay O’ là trung điểm BJ

Vì OO’ là đường trung bình của ΔABJ nên OO’ // AJ

Mà AJ ⊥ (SBC) nên OO’ ⊥ (SBC)

c) Ta có (SCD) ∩ (ABCD) = CD.

Gọi M = JK ∩ CD

SA ⊥ (ABCD) ⇒ SA ⊥ AM(⊂ (ABCD)) (5)

SB ⊥ (P) ⇒ SB ⊥ AM (⊂ (P)) (6)

Từ (5) và (6), ta có: AM ⊥ (SAB) ⇒ AM ⊥ AB.

Suy ra AM là tiếp tuyến của đường tròn ngoại tiếp ΔABC tại A. Như vậy AM cố định. Vì M = AM ∩ CD nên M cố định.

d) ΔAIB vuông tại I nên OA = OB = OI

ΔAJB vuông tại J (do AJ ⊥ (SBC)) nên OA = OB = OJ).

ΔAKB vuông tại K (do AK ⊥ (SBD)) nên OA = OB = OK).

Ta có OA = OB = OC = OD = OI = OJ = OK nên O là điểm cách đều các điểm đã cho và OA = AB/2 = a.

e) Theo chứng minh câu c.

f) Khi S thay đổi trên d, ta có I luôn nằm trong mặt phẳng (B, d).

Trong mặt phẳng này I luôn nhìn đoạn AB cố định dưới góc vuông nên tập hợp I là đường tròn ( C 1 ) đường kính AB nằm trong mặt phẳng (B, d).

Tương tự, tập hợp J là đường tròn ( C 2 ) đường kính AC nằm trong mặt phẳng (C, d) và tập hợp K là đường tròn đường kính AD nằm trong mặt phẳng (D, d).

Hs lớp 12 không biết lên mạng tra xem có không rồi mới hỏi à.-.