Phát biểu định nghĩa tính chất 3 đường trung tuyến của tam giác vẽ hình và ghi giả thuyết kết luận

Những câu hỏi liên quan
Phát biểu định nghĩa đường trung tuyến của tam giác vẽ hình và ghi giả thiết kết luận
Định nghĩa: là đường thẳng nối từ đỉnh đến trung điểm của cạnh đối diện trong tam giác
Đúng 1
Bình luận (0)
1. Phát biểu, vẽ hình, ghi giả thiết - kết luận của định lí Ta-let, định lí đảo, hệ quả
2. Phát biểu, vẽ hình, ghi giả thiết - kết luận của tính chất đường phân giác trong tam giác
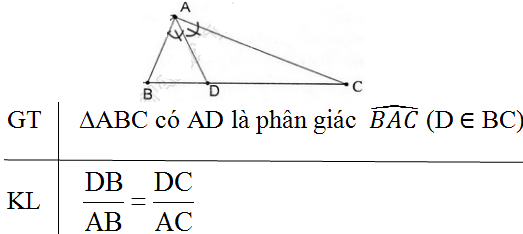
Phát biểu định lí về tính chất của đường phân giác trong tam giác (vẽ hình, ghi giả thiết và kết luận).
Định lý:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn ấy.
Đúng 0
Bình luận (0)
Nêu các trường hợp bằng nhau của hai tam giác, hai tam giác vuông? Vẽ hình, ghi giảthuyết, kết luận cho từng trường hợp?2. Nêu định nghĩa, tính chất của tam giác cân, tam giác đều?3. Nêu định lý Pytago thuận và đảo, vẽ hình, ghi giả thuyết, kết luận của cả hai định lý4. Nêu định lý về quan hệ giữa góc và cạnh đối diện trong tam giác, vẽ hình, ghi giả thiết, kết luận.5. Nêu quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, vẽ hình, ghigiả thuyết, kết luận cho từng mối quan hệ....
Đọc tiếp
Nêu các trường hợp bằng nhau của hai tam giác, hai tam giác vuông?
Vẽ hình, ghi giảthuyết, kết luận cho từng trường hợp?
2. Nêu định nghĩa, tính chất của tam giác cân, tam giác đều?
3. Nêu định lý Pytago thuận và đảo, vẽ hình, ghi giả thuyết, kết luận của cả hai định lý
4. Nêu định lý về quan hệ giữa góc và cạnh đối diện trong tam giác, vẽ hình, ghi giả thiết, kết luận.
5. Nêu quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, vẽ hình, ghigiả thuyết, kết luận cho từng mối quan hệ.
6. Nêu định lý về bất đẳng thức trong tam giác, vẽ hình, ghi giả thiết, kết luận
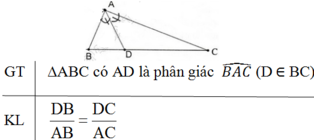
Phát biểu định lí về tính chất của đường phân giác trong tam giác (vẽ hình, ghi giả thiết và kết luận) ?
Định lý:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn ấy.
Đúng 0
Bình luận (0)
1. Nêu các trường hợp bằng nhau của hai tam giác thường, hai tam giác vuông? Vẽ hình,gi giả thuyết kết luận?
2. Nêu định nghĩa, tính chất tam giác cân, tam giác đều?
3. Nêu định lý Pytago thuận và đảo, vẽ hình ghi giả thuyết, kết luận?
4. Nêu định lý về quan hệ giữa góc và đường xiên, đường xiên và hình chiếu, vẽ hình, ghi giả thuyết, kết luận
5. Nêu quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, ghi giả thuyết, kết luận
6. Nêu định lý về bắt đẳng thức trong tam giác vẽ hì...
Đọc tiếp
1. Nêu các trường hợp bằng nhau của hai tam giác thường, hai tam giác vuông? Vẽ hình,gi giả thuyết kết luận?
2. Nêu định nghĩa, tính chất tam giác cân, tam giác đều?
3. Nêu định lý Pytago thuận và đảo, vẽ hình ghi giả thuyết, kết luận?
4. Nêu định lý về quan hệ giữa góc và đường xiên, đường xiên và hình chiếu, vẽ hình, ghi giả thuyết, kết luận
5. Nêu quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, ghi giả thuyết, kết luận
6. Nêu định lý về bắt đẳng thức trong tam giác vẽ hình, ghi giả thuyết kết luận
7. Nêu tính chất 3 đường trung tuyến trong tam giác vẽ hình, ghi giả thuyết, kết luận
8. Nêu tính chất đường phân giác của một góc, tính chất 3 đường phân giác của tam giác, vẽ hình, ghi giả thuyết, kết luận
9. Nêu tính chất đường trung trực của một đoạn thẳng, tính chất 3 đường trung trực của tam giác, vẽ hình, ghi giả thuyết, kết luận
1.tam giác thường (cạnh.cạnh.cạnh)(cạnh.góc.cạnh)(góc .cạnh.góc)
tam giác vuông:
Nếu cạnh huyền và môt cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
- Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau(theo trường hợp c.g.c)
- Nếu một cạnh của tam giác vuông này và một góc nhọn kề cạnh ấy bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Đúng 0
Bình luận (0)
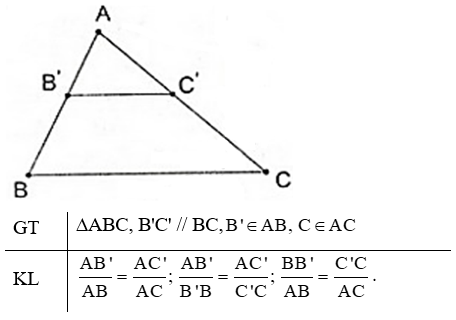
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Talet trong tam giác.
Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
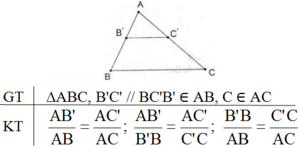
Đúng 0
Bình luận (0)
2 : Phát biểu tính chất : " Hai tia phân giác của 2 góc kề bù tạo thành góc vuông " thành định lí dạng : Nếu.... thì
rồi vẽ hình và ghi Giả thiết , kết luận của định lí
Chứng minh định lí và phát biểu
Nếu Ox,Oy là hai tia phân giác của hai góc kề bù thì Ox\(\perp Oy\)
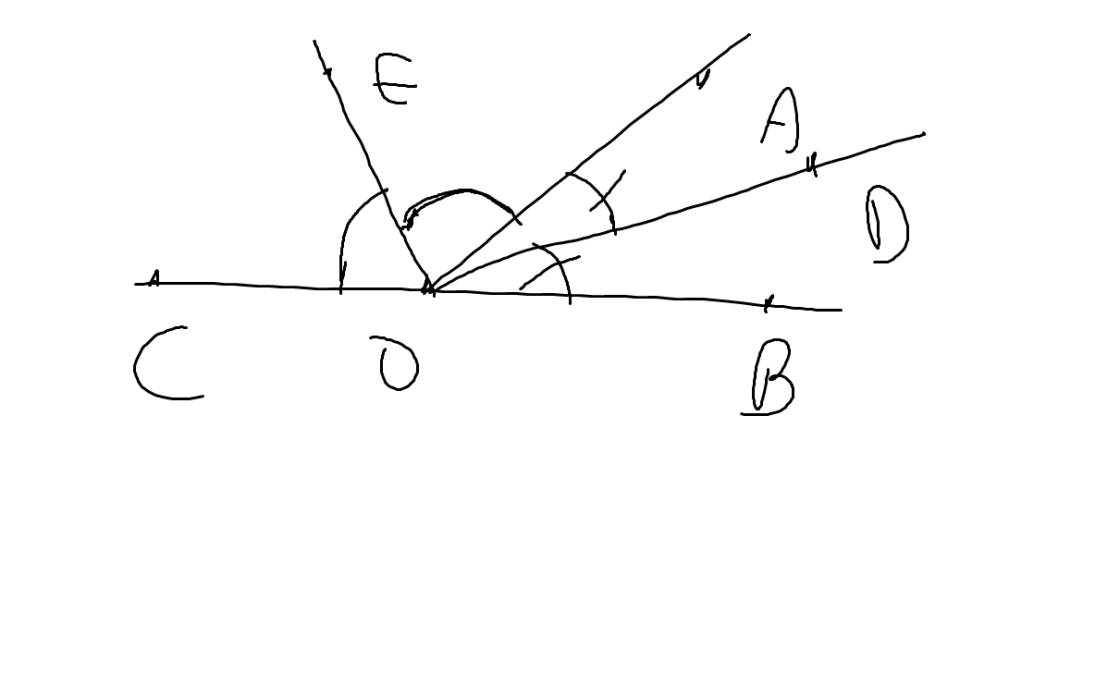
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù OD,OE lần lượt là phân giác của \(\widehat{AOB};\widehat{AOC}\) |
| KL | OD\(\perp\)OE |
OD là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOB}=2\cdot\widehat{AOD}\)
OE là phân giác của \(\widehat{AOC}\)
=>\(\widehat{AOC}=2\cdot\widehat{AOE}\)
\(\widehat{AOB}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOE}+2\cdot\widehat{AOD}=180^0\)
=>\(\widehat{AOE}+\widehat{AOD}=90^0\)
=>\(\widehat{EOD}=90^0\)
=>OE\(\perp\)OD(ĐPCM)
Đúng 5
Bình luận (0)
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta - lét trong tam giác ?
Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Đúng 1
Bình luận (0)