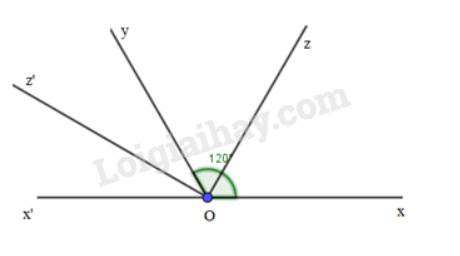
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ  = 60^\circ \)

Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ  = 30^\circ \)

Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} =  60^\circ  + 30^\circ  = 90^\circ \)

Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)

Chú ý:

2 tia phân giác của 2 góc kề bù thì vuông góc với nhau

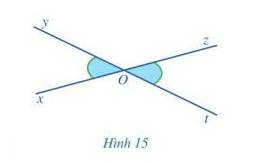
a) Cách 1: Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz nằm về hai phía đối với đường thẳng chứa tia Oy nên hai góc xOy và yOz là hai góc kề nhau. Hơn nữa, hai góc xOy và yOz có tổng bằng góc xOz =180 độ nên hai góc xOy và yOz là hai góc bù nhau.

Vậy hai góc xOy và yOz là hai góc kề bù

Cách 2: Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz là hai tia đối nhau nên hai góc xOy và yOz là hai góc kề bù.

b) Cách 1: Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot nằm về hai phía đối với đường thẳng chứa tia Oz nên hai góc yOz và zOt là hai góc kề nhau. Hơn nữa, hai góc yOz và zOt có tổng bằng góc xOz =180 độ nên hai góc yOz và zOt là hai góc bù nhau.

Vậy hai góc yOz và zOt là hai góc kề bù

Cách 2: Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot là hai tia đối nhau nên hai góc yOz và zOt là hai góc kề bù.

c) Do

\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} = \widehat {xOz} = 180^\circ ;\\\widehat {yOz} + \widehat {zOt} = \widehat {yOt} = 180^\circ \end{array}\)

Vậy \(\widehat {xOy} + \widehat {yOz} = \widehat {yOz} + \widehat {zOt}\)

\( \Rightarrow \widehat {xOy} = \widehat {zOt}\)

Chú ý: Ta có thể dùng dấu hiệu sau: 2 góc kề bù khi có chung đỉnh, chung một cạnh, 2 cạnh còn lại là 2 tia đối nhau.

vì góc xOy và yOz là 2gocs kề bù                      vì tia ot là tia phân giác của yOz   nênyOt=tOz=yOz/2=120/2=60

Nên xOy+yOz=180                                        góc xOy và yOz là 2 góc kề bù mà tia ot là tia phân giác của yOz

                                                                        nên tia oy nằm giữa tiaox,ot

60+yOz=180                                                   vậy tia oy là tia phân giác của góc zOt vì+tia oy nằm giữa oz,oz

yOz=180-60=120                                                                                                        +yOt=xOy=60

Vẽ hình bn tự vẽ nha....

a, Có góc xOy và góc yOz là 2 góc kề bù nên suy ra xOy+yOz=180 độ

60+yOz=180(vì xOy=60)

yOz=180-60

yOz=120

Vậy góc yOZ bằng 120 độ

Đề bài sai à bạn? S k vẽ hình đc câu b vậy?

Vì hai góc \(\widehat {xOy},\widehat {yOz}\) kề bù với nhau nên

\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} = 180^\circ \\ \Rightarrow 25^\circ  + \widehat {yOz} = 180^\circ \\ \Rightarrow \widehat {yOz} = 180^\circ  - 25^\circ  = 155^\circ \end{array}\)

a) Ta có \(\widehat{xOy}\) và \(\widehat{yOz}\) là 2 góc kề bù (theo đề)
   \(\Rightarrow\widehat{xOy}+\widehat{yOz}=180^0\)
   Hay \(50^0+\widehat{yOz}=180^0\)
                   \(\Rightarrow\widehat{yOz}=130^0\)

b) Góc mOn ..... bn tự lm ik
 Ta có: Om là tia phân giác của \(\widehat{xOy}\) (theo đề)
 \(\Rightarrow\)\(\widehat{xOm}=\widehat{yOm}=\frac{\widehat{xOy}}{2}=\frac{50^0}{2}=25^0\)
Lại có : On là tia phân giác của \(\widehat{yOz}\) (theo đề)
\(\Rightarrow\)\(\widehat{yOn}=\widehat{zOn}=\frac{\widehat{yOz}}{2}=\frac{130^0}{2}=65^0\)
Ta lại có: \(\widehat{mOy} + \widehat{nOy} = 25^0 + 65^0 = 90^0\)
 Do đó 2 góc mOy và nOy phụ nhau.

Bài 2:
\(a.\)Vì \(\widehat{xOy}\)kề bù với góc \(\widehat{yOz}\)\(\Rightarrow\)\(\widehat{xOy}+\widehat{yOz}=180^0\)
                                                            \(\Rightarrow\)  \(60^0+\widehat{yOz}=180^0\)
                                                            \(\Rightarrow\)                \(\widehat{yOz}=180^0-60^0=120^0\)
\(b.\) Vì \(Ot\)là tia phân giác \(\widehat{xOy}\)\(\Rightarrow\)\(\widehat{tOy}=\frac{\widehat{xOy}}{2}=\frac{60^0}{2}=30^0\)
         Vì \(Om\)là tia phân giác \(\widehat{yOz}\)\(\Rightarrow\)\(\widehat{yOm}=\frac{\widehat{yOz}}{2}=\frac{120^0}{2}=60^0\)
  Vì \(Oy\)nằm giữa 2 tia \(Ot\)và \(Om\) \(\Rightarrow\) \(\widehat{tOy}+\widehat{yOm}=\widehat{tOm}\)
                                                                    \(\Rightarrow\) \(30^0+60^0=\widehat{tOm}\)
                                                                    \(\Rightarrow\)               \(90^0=\widehat{tOm}\)
                  Vậy \(\widehat{tOm}\)là góc vuông

Bài 2:       Vì góc xOy và yoz kề bù nên góc xOz= 180 độ                                                                                                                             Ta có :                                                                                                                                                                                                          Góc xoy + góc yoz = xOz                                                                                                                                                    Hay :       60 độ  +  góc yoz   = 180 độ                                                                                                                                                                         góc yoz = 180 độ - 60 độ = 120 độ                                                                                                                                       Vậy....

Vì\(\widehat{xOy}\)và\(\widehat{yOz}\)là hai góc kề bù

Do đó\(\widehat{xOy}+\widehat{yOz}=180^o\)

Hay\(120^o+\widehat{yOz}=180^o\)

\(\Rightarrow\widehat{yOz}=180^o-120^o\)

\(\Rightarrow\widehat{yOz}=60^o\)

Vì tia Ot là tia phân giác của\(\widehat{yOz}\)

\(\Rightarrow\widehat{yOt}=\widehat{zOt}=\frac{\widehat{yOz}}{2}=\frac{60^o}{2}=30^o\)

Vì tia Ot nằm giữa \(\widehat{yOz}\)

Vì Oy nằm giữa\(\widehat{xOz}\)

Do đó tia Oy nằm giữa \(\widehat{xOt}\)

Nên\(\widehat{xOy}+\widehat{yOt}=\widehat{xOt}\)

Hay\(120^o+30^o=\widehat{xOt}\)

\(\Rightarrow\widehat{xOt}=150^o\)

Giải:

Hai góc xOy và x'Oy là hai góc kề bù mà = 100⁰ nên = 180⁰ - 100⁰ = 80⁰.

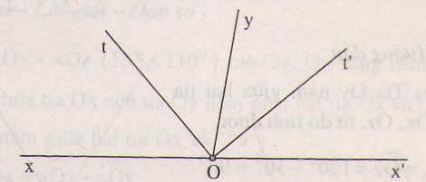
Giải tương tự bài 33, ta được ,

hi còn ở đây ko

gần 1 thập kỷ rồi