cho tam giác abc. o nằm trong tam giác. qua o kẻ đường thẳng song song với bc cắt ab, ac ở m, n, đường thẳng song song với ca cắt ba, bc ở f, k, đường thẳng song song với ab cắt ca, cb ở d,e. chứng minh af/ab + be/bc + cn/ca = 1

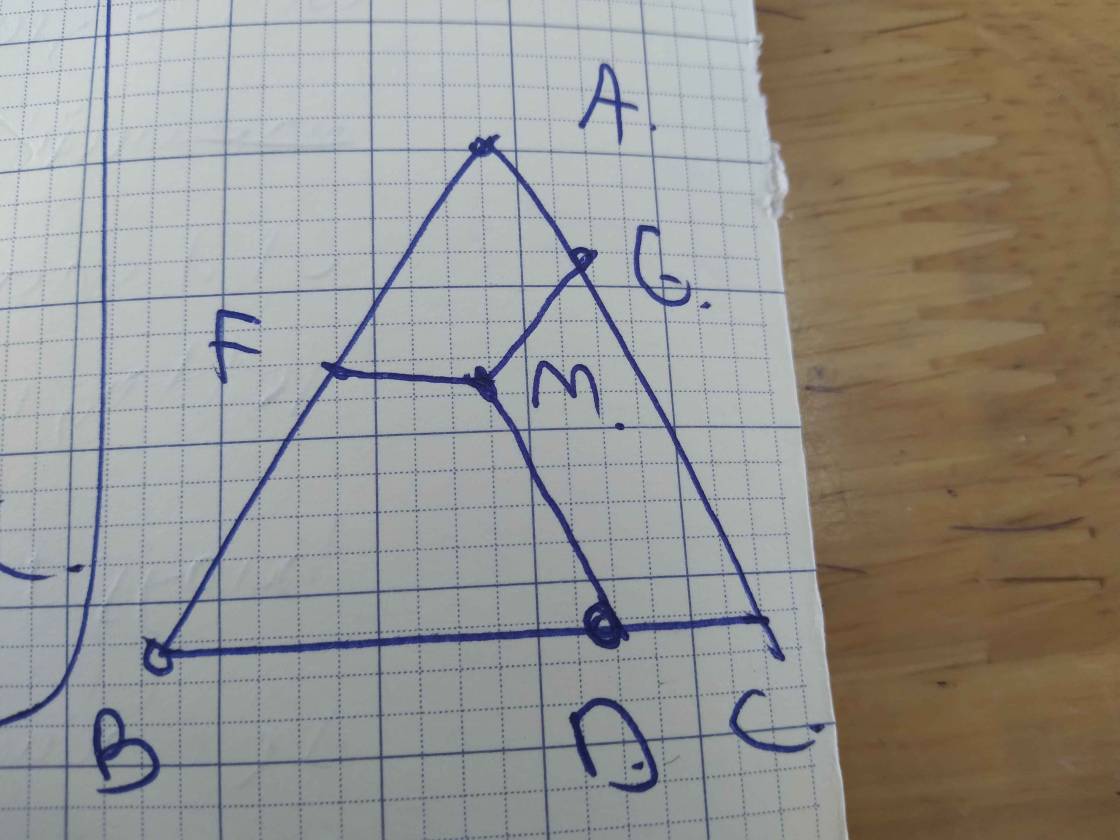
 Bài1: Cho tam giác ABC đều,điểm M nằm trong tam giác ABC,đường thẳng qua M song song với AC cắt BC tại D,đường thẳng qua M song song với BC cắt AB tại E,đường thẳng qua M song song với AB cắt AC tại F . Chứng minh :

a,c/m các tứ giác BEMD,AFME,DMFC là các hình thang cân 

b,độ dài 3 cạnh của tam giác bằng độ dài 3 cạnh của tam giác nào 

Bài1: Cho tam giác ABC đều,điểm M nằm trong tam giác ABC,đường thẳng qua M song song với AC cắt BC tại D,đường thẳng qua M song song với BC cắt AB tại E,đường thẳng qua M song song với AB cắt AC tại F . Chứng minh :

a,c/m các tứ giác BEMD,AFME,DMFC là các hình thang cân 

b,độ dài 3 cạnh của tam giác bằng độ dài 3 cạnh của tam giác nào 

Cho tam giác ABC. Đường phân giác góc A cắt BC tại E.Qua E kẻ đường thẳng song song với AB tại F,qua F kẻ đường thẳng song song với BC cắt AB tại P.CMR:AP=AF

Cho tam giác ABC đều, M là điểm nằm trong tam giác đó. Qua M kẻ đường thẳng song song với AC và cắt BC ở D , kẻ đường thẳng song song với AB cắt AC  tại E , kẻ đường thẳng song song với BC và cắt AB ở F . CM 

A) Từ giác BFMD, CDME, AEMF là các hình thang cân .

B) tính số đo DME, EMF, DMF

Cho tam giác ABC và O thuộc miền trong của tam giác. Đường thẳng qua O song song với AB cắt BC, AC tại D và G. Đường thẳng qua O song song với AC cắt BC, AB tại E và H. Đường thẳng qua O song song với BC cắt BA, AC tại K và F. Tính diện tích BKOD theo diện tích tam giác HOK và diện tích tam giác ODE.

Cho tam giác ABC đều .Từ điểm O trong tam giác đó kẻ đường thẳng song song với BC cắt AC ỏ D ,kẻ đường thẳng song song với AB cắt BC ở E , kẻ đường thẳng thẳng song song với AC cắt AB ở F 

SO sánh chu vi của tam giác DEF với tổng độ dài các đoạn OA,OB,OC

Cho tam giác ABC biết AB=5cm, BC=10cm. Lấy điểm D trên cạnh AB sao cho AD=3cm. Qua D kẻ đường thẳng song song với BC cắt AC tại E

a.Tính độ dài DE

b. Qua C kẻ đường thẳng song song với AB cắt tia DE tại G. Chứng minh tam giác ADE đồng dạng với tam giác CGE và AD.AE=DB.DE

c. Đường thẳng BG cắt AC tại H. Chứng minh HC² = HE. HA

cho tam giác ABC phân giác AD qua D kẻ đường thẳng song song với AB cắt AC ở E qua E kẻ đường thẳng song song với BC cắt AB ở K c/m a tam giác ADE cân b AE= BK

cho tam giác abc M là trung điểm của AB. đường thẳng kẻ qua M và song song với BC, cắt AC ở E,đường thẳng kẻ qua E và song song với AB cắt BC ở F:

a)AM=EF

b)tam giác AME=tam giác EFC

c)AE=EC và BF=FC