xác định dư của phép chia đa thức :
x20 +x11 - x2016 cho đa thức x2-1
Phần dư của phép chia đa thức x 2 + 3 x + 2 5 + x 2 - 4 x - 4 5 - 1 cho đa thức x + 1 là
A. 3
B. 2
C. 0
D. 1
Ta có đa thức x 2 + 3 x + 2 5 + x 2 - 4 x - 4 5 - 1 chưa (x + 1) nên phần dư là một hằng số
Gọi thương là Q(x) và dư r. Khi đó với mọi x ta có
x 2 + 3 x + 2 5 + x 2 - 4 x - 4 5 - 1 = Q(x)(x + 1) + r (1)
Thay x = -1 vào (1) ta được
( ( - 1 ) 2 + 3 . ( - 1 ) + 2 ) 5 + ( ( - 1 ) 2 – 4 ( - 1 ) – 4 ) 5 – 1 = Q(x).(-1 + 1) + r
r = 0 5 + 1 5 – 1 ó r = 0
vậy phần dư của phép chia là r = 0.
đáp án cần chọn là: C
Tìm dư của phép chia đa thức x2022-x2021+2020 cho đa thức x2-1
Xác định số dư của phép chia đa thức x^16 + x^5 - x^1995 cho đa thức x^2-1
các câu giúp mình với
nếu mình học lớp 8 rồi thì mình giải giúp cho bạn
Xác định số dư của phép chia đa thức x^16 + x^5 - x^1995 cho đa thức x^2-1
các câu giúp mình với
mk chịu
@@
Phép chia đa thức ( 4 x 4 + 3 x 2 – 2x + 1) cho đa thức x 2 + 1 được đa thức dư là:
A. 2x + 2
B. -2x + 2
C. -2x - 2
D. 3 - 2x
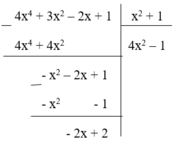
Vậy đa thức dư là R = -2x + 2
Đáp án cần chọn là: B
Phần dư của phép chia đa thức x 4 – 2 x 3 + x 2 – 3x + 1 cho đa thức x 2 + 1 có hệ số tự do là
A. 2
B. 3
C. 1
D. 4

Đa thức dư là – x + 1 có hệ số tự do là 1.
Đáp án cần chọn là: C
Cho hai đa thức A=8x3+2x2-8x-5 và đa thức B=4x+1
a) Thực hiện phép chia đa thức A cho đa thức B. Xác định đa thức thương M và phần dư N
\(\dfrac{A}{B}=\dfrac{8x^3+2x^2-8x-2-3}{4x+1}\)
\(=2x^2-2-\dfrac{3}{4x+1}\)
Không làm phép chia, tìm phần dư trong đa thức f(x) cho đa thức g(x) trong:
f(x)= x+x5+x10+x20 ; g(x) = x2-1
Do đa thức chia có bậc 2
nên đa thức dư là nhị thức bậc nhất
Đặt đa thức dư là \(ax+b\)
Đa thức thương là \(Q_{\left(x\right)}\)
\(\Rightarrow x+x^5+x^{10}+x^{20}=\left(x^2-1\right)Q_{\left(x\right)}+ax+b\\ \Leftrightarrow\left(x+1\right)\left(x-1\right)Q_{\left(x\right)}+ax+b\)
Đẳng thức trên luôn đúng \(\forall x\)
nên lần lượt cho \(x=1;x=-1\)
\(\text{Ta được : }\left\{{}\begin{matrix}a+b=4\\b-a=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{4-0}{2}\\b=\dfrac{4+0}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=2\\b=2\end{matrix}\right.\)
\(\Rightarrow ax+b=2x+2\)
Vậy số dư trong phép chia \(f_{\left(x\right)};g_{\left(x\right)}\)
là \(2x+2\)
Phép chia đa thức 2 x 4 – 3 x 3 + 3 x – 2 cho đa thức x 2 – 1 được đa thức dư là
A. 0
B. 1
C. 2
D. 10
xác định dư của phép chia đa thức :
x20+ x11 - x2016 cho đa thức x2 - 1
Xác định số dư của phép chia đa thức
x19 + x5 - x1995 cho đa thức x2 - 1
Bài này trên violimpic à?
Quen thế.
\(A\left(x\right)=x^{19}+x^5-x^{1995}\)
\(Q\left(x\right)=x^2-1\)
\(A\left(x\right)=Q\left(x\right)+r\)
\(<=>x^{19}+x^5-x^{1995}=\left(x^2-1\right)+r\)
Điều này đúng với mọi x thuộc R
Vậy ta có x=1
=> 1+1+1=0+r
=>r=3
Vậy số dư là 3
Cách mình làm là phương pháp giá trị riêng, một phương pháp cực hay trong toán chia hết của các đa thức.
Nó còn là một định lí là định lí Bơzu.
Nhưng trong chương trình phổ thông, nó là phương pháp giá trị riêng.