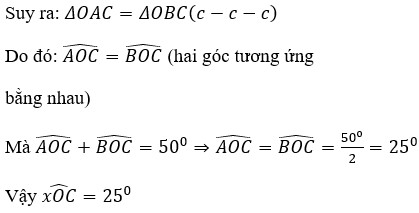Cho \(\widehat{xOy}\)< 90o. Vẽ đường tròn tâm O bán kính R lần lượt cắt Ox tại A; Oy tại B. Qua A kẻ đường thẳng vông góc với Ox và cắt Oy tại C. Qua B kẻ đường thẳng vuông góc với Oy và cắt Ox tại D. AC cắt BD tại E. C/m ΔAOE=ΔBOE

Những câu hỏi liên quan
Cho
x
O
y
^
50
o
, vẽ cung tròn tâm O bán kính 2 cm, cung tròn này cắt Ox và Oy lần lượt ở A và B. Vẽ các cung tròn bán kính tâm A và B có bán kính 3 cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính
x
O
C
^
A. 50
°
B. 25
°
C. 8...
Đọc tiếp
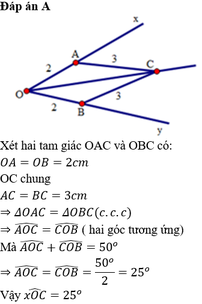
Cho x O y ^ = 50 o , vẽ cung tròn tâm O bán kính 2 cm, cung tròn này cắt Ox và Oy lần lượt ở A và B. Vẽ các cung tròn bán kính tâm A và B có bán kính 3 cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính x O C ^
A. 50 °
B. 25 °
C. 80 °
D. 90 °
Cho
x
O
y
^
60
o
, vẽ cung tròn tâm O bán kính 3 cm, cung tròn này cắt Ox và Oy lần lượt ở A và B. Vẽ các cung tròn bán kính tâm A và B có bán kính 4 cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính
x
O
C
^
A. 60
°
B. 30
°
C. 4...
Đọc tiếp
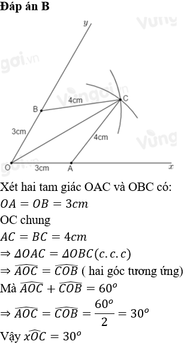
Cho x O y ^ = 60 o , vẽ cung tròn tâm O bán kính 3 cm, cung tròn này cắt Ox và Oy lần lượt ở A và B. Vẽ các cung tròn bán kính tâm A và B có bán kính 4 cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính x O C ^
A. 60 °
B. 30 °
C. 45 °
D. 40 °
Cho
x
O
y
^
50
°
, vẽ cung tròn tâm O bán kính bằng 2cm, cung tròn này cắt Ox, Oy lần lượt tại A và B. Vẽ các cung tròn tâm A và B bán bính bằng 3cm, cắt nhau tại điểm C nằm trong
x
O
y
^
. Tính
x
O
C
^...
Đọc tiếp
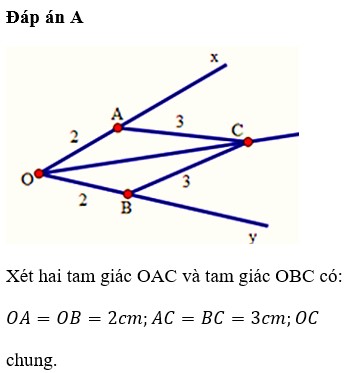
Cho x O y ^ = 50 ° , vẽ cung tròn tâm O bán kính bằng 2cm, cung tròn này cắt Ox, Oy lần lượt tại A và B. Vẽ các cung tròn tâm A và B bán bính bằng 3cm, cắt nhau tại điểm C nằm trong x O y ^ . Tính x O C ^
A. 25
B. 50
C. 80
D. 90
cho góc xOy và tia Am
vẽ cng tròn tâm O bán kính r , cung này cắt Ox và Oy ở B và C .Vẽ cung tròn tâm A bán kính r , cung này cắt tia Am tại D . Vẽ cung tròn tâm D bán kính BC , cung này cắt cung tròn tâm A bán kính r tại E . CMR GÓC DAE = GÓC xOy
cho đường tròn tâm O bán kính R và 1 điểm A sao cho OA=R√ 2 . vẽ các tiếp tuyến AB, AC với các đường tròn 1 góc XOY= 45 độ cắt AB và AC lần lượt tại D và E. C/M DE là tiếp tuyến của đường tròn tâm O
Cho \(\widehat {xOy}\). Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong \(\widehat {xOy}\). Nối O với P (Hình 16). Hãy chứng minh rằng , từ đó suy ra OP là tia phân giác của \(\widehat {xOy}\).
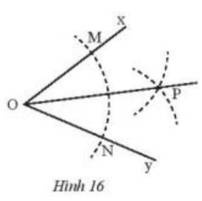
Vì M, N thuộc đường tròn tâm O có cùng bán kính nên OM = ON = bán kính cung tròn tâm O
Từ M, N vẽ 2 cung tròn có cùng bán kính và 2 đường tròn cắt nhau tại P
Suy ra P thuộc cả 2 cung tròn tâm M, N có cùng bán kính nên MP = NP
Xét tam giác OMP và tam giác ONP ta có :
OM = ON
OP cạnh chung
MP = NP
\(\Rightarrow \Delta{OMP}=\Delta{ONP}\) ( c-c-c )
\( \Rightarrow \widehat {MOP} = \widehat {PON}\) (2 góc tương ứng)
Do đó, OP là phân giác \(\widehat {xOy}\)
Đúng 0
Bình luận (0)
Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy1.Vẽ đường tròn tâm O, cắt Ox và Oy lần lượt tại A và B.2.Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.3. Vē tia Oz đi qua M.Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
Đọc tiếp
Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy
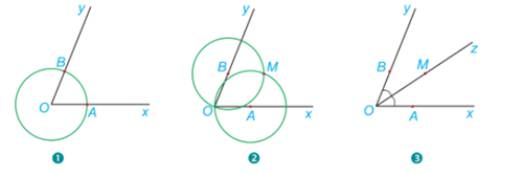
1.Vẽ đường tròn tâm O, cắt Ox và Oy lần lượt tại A và B.
2.Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.
3. Vē tia Oz đi qua M.
Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
Xét \(\Delta OBM\) và \(\Delta OAM\) có:
\(OA = OB( = R)\)
OM chung
AM=BM (do hai đường tròn tâm A và B có bán kính bằng nhau)
\( \Rightarrow \)\(\Delta OBM\) = \(\Delta OAM\)(c.c.c)
\( \Rightarrow \) \(\widehat {MOB} = \widehat {MOA}\) (hai góc tương ứng)
Mà tia OM nằm trong góc xOy
Vậy OM là tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
Cho góc xOy và tia Am ( h.74a). Vẽ cung tròn tâm O bán kính r, cung này cắt Ox, Oy theo thứ tự ở B, C. Vẽ cung tròn tâm A bán kính r, cung này cắt tia Am ở D (h.74b).Vẽ cung tròn tâm D có bán kính bằng BC, cung này cắt cung tròn tâm A, bán kính r ở E (h.74c). Chứng minh rằng góc DAE góc xOy
Đọc tiếp
Cho góc xOy và tia Am ( h.74a).
Vẽ cung tròn tâm O bán kính r, cung này cắt Ox, Oy theo thứ tự ở B, C. Vẽ cung tròn tâm A bán kính r, cung này cắt tia Am ở D (h.74b).Vẽ cung tròn tâm D có bán kính bằng BC, cung này cắt cung tròn tâm A, bán kính r ở E (h.74c).
Chứng minh rằng góc DAE = góc xOy
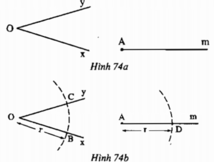
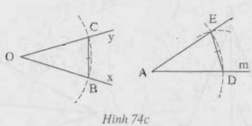
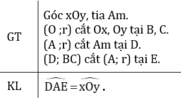
Kí hiệu: (O ;r) là đường tròn tâm O bán kính r.
B, C thuộc (O; r) nên OB = OC = r.
D thuộc (A;r) nên AD = r.
E thuộc (D; BC) và (A;r) nên AE = r, DE = BC.
Xét OBC và ADE có:
OB = AD (cùng bằng r)
OC = AE (cùng bằng r)
BC = DE
Nên ΔOBC = ΔADE (c.c.c)
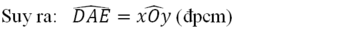
Đúng 0
Bình luận (0)
Cho góc xOy nhọn, vẽ cung tròn tâm O, bán kính r, cắt Ox, Oy tại B, C và các cung tròn tâm B, tâm C có cùng bán kính sao cho chúng cắt nhau ở A nằm trong góc xOy. Nối OA. Chứng minh OA là tia phân giác của góc xOy
Cho góc nhọn xOy, vẽ cung tròn tâm O, bán kính r cắt Ox, Oy tại B,C và các cung tròn tâm B, tâm C có cùng bán kính sao cho chúng cắt nhau ở A nằm trong góc xOy. Nối OA. Chứng minh: OA là tia phân giác của góc xOy