cho tam giác ABC vuông tại A. Biết tanC= 0.75. Không tính số đo góc, tính cotC, sinC, cosC

Những câu hỏi liên quan
cho tema giác abc vuông tại a
a, biết tanC=0,75.Không tính số đo góc a ,hãy tính cosC,sinC,cotC
b, nếu cho cosB=0,8.Tính tanC,sinC,cotC
a) tan=sin/cos=3/4=>cot=1/tan=4/3
=>sin=3/4cos
mà sin2+cos2=1=>cos=0,8
=>sin=2/5
b) dễ hơn a)
có cos=>sin
tan=sin/cos
cot=1/tan
Đúng 0
Bình luận (0)
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
Đúng 0
Bình luận (9)
a) Xét \(\Delta ABC\) vuông tại `A`
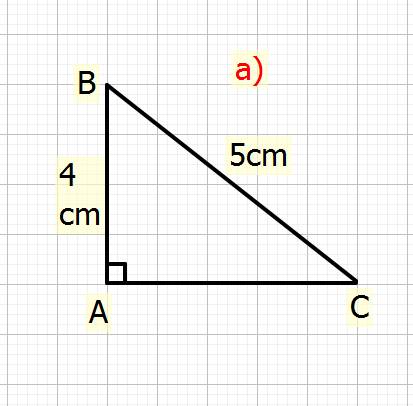
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
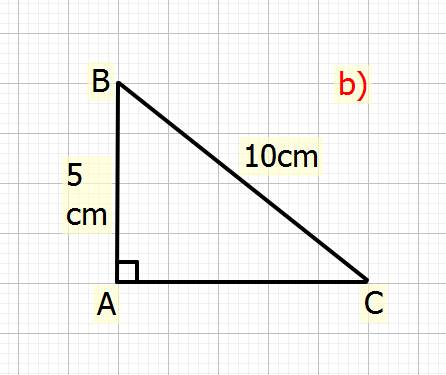
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
Đúng 1
Bình luận (2)
Cho tam giác ABC vuông tại A, AC = 28cm, Tính độ dài các đoạn thẳng AB, BC biết:
a) cotC = \(\frac{7}{11}\)
b) tanC = \(\frac{5}{7}\)
c) cosC = \(\frac{4}{5}\)
d) sinC = \(\frac{3}{5}\)
a, Xét tam giác ABC vuông tại A, đường cao AH
cotC = 7/11 => \(\frac{AB}{AC}=\frac{7}{11}\Rightarrow AB=\frac{7}{11}.AC=\frac{7}{11}.28=\frac{196}{11}\)cm
Theo định lí Pytago cho tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\frac{196}{11}\right)^2+28^2}=33,188...\)cm
b, tanC = 5/7 => \(\frac{AC}{AB}=\frac{5}{7}\Rightarrow AB=\frac{7}{5}AC=\frac{7}{5}.28=\frac{196}{5}\)cm
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\frac{196}{5}\right)^2+28^2}=\frac{28\sqrt{74}}{5}\)cm
c, cosC = 4/5 => \(\frac{AC}{BC}=\frac{4}{5}\Rightarrow BC=\frac{5}{4}AC=\frac{5}{4}.28=35\)cm
Theo định lí Pytago tam giác ABC vuông tại A
\(AB=\sqrt{BC^2-AC^2}=21\)cm
d, sinC = 3/5 => \(\frac{AB}{BC}=\frac{3}{5}\Rightarrow\frac{AB}{3}=\frac{BC}{5}\Rightarrow\frac{BC^2}{25}=\frac{AB^2}{9}\)
Theo tính chất dãy tỉ số bằng nhau
\(\frac{BC^2}{25}=\frac{AB^2}{9}=\frac{BC^2-AB^2}{25-9}=\frac{AC^2}{16}=49\)
\(\Rightarrow BC=35cm;AB=21cm\)
: Tam giác ABC vuông tại A. Khẳng định nào sau đây đúng?
A. sinB = sinC B. cosB = cosC C. tanB = cotC D. cotB = cotC
cho △ ABC vuông tại A ,CMR: , TanB=cotC,cotB=Tanc
CoSB=sinC , TanB=cotC,cotB=Tanc
Cho tam giác ABC vuông tại A biết AB=6cm,BC=10cm. Tính SinB+CosB/TanC+CotC
cho △ ABC vuông tại A ,CMR:CoSB=sinC , TanB=cotC,cotB=Tanc
CosB = AB / BC
SinC = AB / BC
=> CosB = SinC
Tương tự em làm các bài sau nhé !
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a đường cao ah. biết AH= 4,HC=5 tính tanC và số đo góc B
`tanC = (AH)/(HC) = 4/5`
Áp dụng định lý Pytago:
`AC^2 = AH^2+HC^2`
`=> AC=\sqrt41`
Áp dụng hệ thức lượng trong tam giác:
`AH^2=HB.HC`
`=> HB=16/5`
Có: `tanB = (AH)/(HB) = 4/(16/5)=5/4`
`=> \hatB ≈51^o`
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, có AH là đường cao.1. Biết AH 2/6 cm, BH 4 cm.a) Tính độ dài các đoạn thẳng HC, ACb) Tính số đo góc ABH (làm tròn đến độ)2. Cho AC 3 .AB. Chứng minh: 3.tan C-cotC+ /sinC sin 45°3. Lấy điểm M trên đường tròn tâm B bán kính BA (M thuộc nửa mặt phẳng bờ BC, không chứa điểm A). Gọi SBMH là diện tích tam giác BMH, Sạc là diện tích tam giác BCM. Chứng minh rằng: SaMH SHCM .sinº ACB
Đọc tiếp
Cho tam giác ABC vuông tại A, có AH là đường cao.
1. Biết AH= 2/6 cm, BH = 4 cm.
a) Tính độ dài các đoạn thẳng HC, AC
b) Tính số đo góc ABH (làm tròn đến độ)
2. Cho AC = 3 .AB. Chứng minh: 3.tan C-cotC+ /sinC = sin 45°
3. Lấy điểm M trên đường tròn tâm B bán kính BA (M thuộc nửa mặt phẳng bờ BC, không chứa điểm A). Gọi SBMH là diện tích tam giác BMH, Sạc là diện tích tam giác BCM. Chứng minh rằng: SaMH =SHCM .sinº ACB



















