cho hai đường thẳng a,b song song với nhau và hai đường thẳng c,d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác.
a, CM: An // Cp va Dm // Bq
b, CM: An vuông góc với Bq
Giúp mình với mai kiểm tra 1 tiết rồi.
Thanks nhìu nha.....
Trong các câu sau, câu nào đúng, câu nào sai?
a) Qua điểm A nằm ngoài đường thẳng d, chỉ có một đường thẳng song song với d.
b) Qua điểm A nằm ngoài đường thẳng d, có vô số đường thẳng song song với d.
c) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng a thì hai đường thẳng AB và AC trùng nhau.
d) Nếu qua điểm A có hai đường thẳng cùng song song với đường thẳng d thì hai đường thẳng đó song song với nhau
Chọn các câu khẳng định đúng:
a) Qua điểm A nằm ngoài đường thẳng xy, có một đường thẳng song song với xy.
b) Qua điểm A nằm ngoài đường thằng xy, có duy nhất một đường thẳng song song với xy.
c) Qua điểm A nằm ngoài đường thẳng xy, có vô số đường thẳng song song với xy.
d) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng m thì hai đường thẳng AB và AC trùng nhau.
e) Nếu qua điểm A có hai đường thẳng cùng song song với đường thẳng d thì hai đường thẳng đó song song với nhau
Chọn các câu khẳng định đúng:
a) Qua điểm A nằm ngoài đường thẳng xy, có một đường thẳng song song với xy.
b) Qua điểm A nằm ngoài đường thằng xy, có duy nhất một đường thẳng song song với xy.
c) Qua điểm A nằm ngoài đường thẳng xy, có vô số đường thẳng song song với xy.
d) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng m thì hai đường thẳng AB và AC trùng nhau.
e) Nếu qua điểm A có hai đường thẳng cùng song song vói đường thẳng d thì hai đường thẳng đó song song với nhau
Cho mặt phẳng (α)
chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (β)
(H.4.41)
Nếu (α)và (β) cắt nhau theo giao tuyến c thì hai đường thẳng a và c có song song với nhau hay không, hai đường thẳng b và c có song song với nhau hay không?
Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.
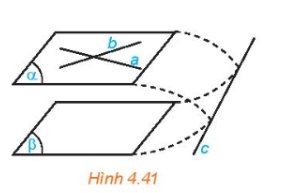
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
Chọn câu đúng trong các câu sau:
a) Qua điểm A nằm ngoài đường thẳng m, có một đường thẳng song song với m.
b) Qua điểm A nằm ngoài đường thẳng m, chỉ có một đường thẳng song song với m.
c) Qua điểm A nằm ngoài đường thẳng m, có duy nhất một đường thẳng song song với m
d) Qua điểm A nằm ngoài đường thẳng d, có hai đường thẳng phân biệt cùng song song với d
e) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng d thì hai đường AB và AC trùng nhau.
f) Nếu hai đường thẳng b và c cùng song song với đường thẳng a thì hai đường thẳng b và c trùng nhau
Cho hai đường thẳng a và b song song với nhau. Một đường thẳng d vuông góc với a và b. Khi đó đường thẳng d có vuông góc với mặt phẳng xác định bởi hai đường thẳng song song a và b không ?
Không vì trái với định lí ( a // b thì a và b không cắt nhau)
Trong các khẳng định sau đây khẳng định nào đúng? khẳng định nào sai?
a) Cho hai đường thẳng a và b song song với nhau. Nếu có một đường thẳng d vuông góc với a thì d vuông góc với b.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau.
c) Một mặt phẳng (α) và một đường thẳng a cùng vuông góc với đường thằng b thì a // (α).
d) Hai mặt phẳng (α) và (β) phân biệt cùng vuông góc với một mặt phẳng (γ) thì (α) // (β).
e) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau.
f) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song.
a) Đúng
b) Đúng
c) Sai
d) Sai
e) Sai
f) Đúng
Trong các câu sau câu nào Sai?
A. Hai đường thẳng vuông góc với nhau thì tạo ra 4 góc vuông.
B. Hai đường thẳng song song là hai đường thẳng không cắt nhau, không trùng nhau.
C. Hai đường thẳng b và c cùng song song với đường thẳng a thì b và c song song.
D. Nếu hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
Cho hình bs 10 (hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).
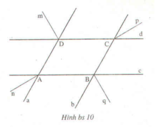
Chứng minh: An vuông góc với Bq.
Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Cho hình bs 10 (hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).
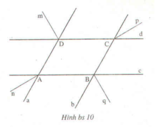
Chứng minh: An // Cp và Dm // Bq.
Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.