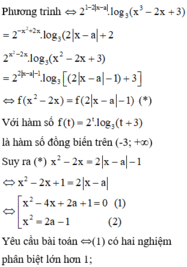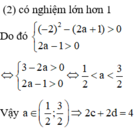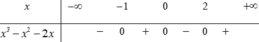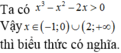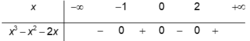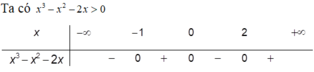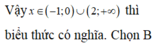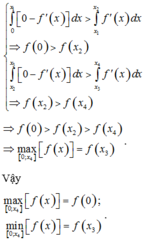tập hợp các giá trị của x , x4+x3+2x-4=0

Những câu hỏi liên quan
Cho phương trình
4
-
x
-
a
.
log
3
x
2
-
2
x
+
3
+
2
-
x...
Đọc tiếp
Cho phương trình 4 - x - a . log 3 x 2 - 2 x + 3 + 2 - x 2 + 2 x . log 1 3 2 x - a + 2 = 0 . Tập tất cả các giá trị của tham số a để phương trình có 4 nghiệm x 1 ; x 2 ; x 3 ; x 4 thỏa mãn là (c;d). Khi đó giá trị biểu thức T = 2 c + 2 d bằng:
A. 5
B. 2
C. 3
D. 4
Cho biểu thức sau :B[(x4−x+x−3x3+1).(x3−2x2+2x−1)(x+1)x9+x7−3x2−3+1−2(x+6)x2+1].4x2+4x+1(x+3)(4−x)[(x4−x+x−3x3+1).(x3−2x2+2x−1)(x+1)x9+x7−3x2−3+1−2(x+6)x2+1].4x2+4x+1(x+3)(4−x)a, Tìm giá trị của x để giá trị của biểu thức B được xác địnhb, Rút gọn Bc, Cmr với các giá trị của x mà giá trị của biểu thức xác định thì −5≤B≤0
Đọc tiếp
Cho biểu thức sau :
B=[(x4−x+x−3x3+1).(x3−2x2+2x−1)(x+1)x9+x7−3x2−3+1−2(x+6)x2+1].4x2+4x+1(x+3)(4−x)[(x4−x+x−3x3+1).(x3−2x2+2x−1)(x+1)x9+x7−3x2−3+1−2(x+6)x2+1].4x2+4x+1(x+3)(4−x)a, Tìm giá trị của x để giá trị của biểu thức B được xác định
b, Rút gọn B
c, Cmr với các giá trị của x mà giá trị của biểu thức xác định thì −5≤B≤0
Tập hợp các giá trị của x để biểu thức
l
o
g
5
(
x
3
–
x
2
-
2
x
)
có nghĩa là
Đọc tiếp
Tập hợp các giá trị của x để biểu thức l o g 5 ( x 3 – x 2 - 2 x ) có nghĩa là
![]()
![]()
![]()
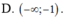
Tập hợp các giá trị của x để biểu thức
log
5
(
x
3
-
x
2
-
2
x
)
có nghĩa là
A
.
(
0
;
1
)
B
.
(
-
1
;
0
)
∪
(...
Đọc tiếp
Tập hợp các giá trị của x để biểu thức log 5 ( x 3 - x 2 - 2 x ) có nghĩa là
A . ( 0 ; 1 )
B . ( - 1 ; 0 ) ∪ ( 2 ; + ∞ )
C . ( 1 ; + ∞ )
D . ( - ∞ ; - 1 )
Tập hợp các giá trị của x để biểu thức
y
log
5
(
x
3
-
x
2
-
2
x
)
có nghĩa là A. (0; 1) B.
(
-
1
;
0
)
∪
(
2
;
+
∞
)
C. ...
Đọc tiếp
Tập hợp các giá trị của x để biểu thức y = log 5 ( x 3 - x 2 - 2 x ) có nghĩa là
A. (0; 1)
B. ( - 1 ; 0 ) ∪ ( 2 ; + ∞ )
C. ( 1 ; + ∞ )
D. ( - ∞ ; - 1 )
Cho các số thực
x
1
,
x
2
,
x
3
,
x
4
thỏa mãn
0
x
1
x
2
x
3
x
4
và hàm số yf(x). Biết hàm số yf’(x) có đồ thị như hình vẽ. Gọi M và m lần...
Đọc tiếp
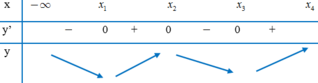
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y=f(x). Biết hàm số y=f’(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
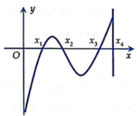
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .
Gọi x1 , x2 là nghiệm của pt x^2+2009x+1=0 và x3,x4 là nghiệm của pt x^2 +2010 +1=0
Tính giá trị biểu thức (x1+x3)(x2+x3)(x1-x4)(x2-x4)
Giả sử tồn tại giá trị
x
4
sao cho
x
4
x
3
x
2
x
1
(
x
4...
Đọc tiếp
Giả sử tồn tại giá trị x 4 sao cho x 4 = x 3 = x 2 = x 1 ( x 4 > 0 , x 4 ∈ ℝ ) . Tìm chính xác giá trị của x 4 biết bán kính mặt cầu ngoại tiếp tứ diện CDEF trong trường hợp này là R = 179 20 ?
A. x 4 = 1
B. x 4 = 1 2
C. x 4 = 17
D. x 4 = 5
tập hợp các giá trị của x thỏa mãn : x4-2x3+10x2-20x = 0
tập hợp các giá trị của x thỏa mãn khác 0: x+x2-x3-x4
x4-2x3+10x2-20x=0 =>x3(x-2)+10x(x-2)=0 =>(x-2)(x3+10x)=0 =>x(x-2)(x2+10)=0
=>x=0 hoặc x=2 hoặc x= - căn 10
Đúng 0
Bình luận (0)
Tìm x
(x-5)2=(3+2x)2
27x3-54x2+36x=9
cho bt x-y=4 và xy=1 tính giá trị của các biểu thức A=x2+y2,B=x3-y3,C=x4+y4
a) \(\left(x-5\right)^2=\left(3+2x\right)^2\)
\(\Rightarrow\left(3+2x\right)^2-\left(x-5\right)^2=0\)
\(\Rightarrow\left(3+2x+x-5\right)\left(3+2x-x+5\right)=0\)
\(\Rightarrow\left(3x-2\right)\left(x+8\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3x-2=0\\x+8=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-8\end{matrix}\right.\)
b) \(27x^3-54x^2+36x=9\)
\(\Rightarrow27x^3-54x^2+36x-9=0\)
\(\Rightarrow27x^3-54x^2+36x-8+8-9=0\)
\(\Rightarrow\left(3x-2\right)^3-1=0\)
\(\Rightarrow\left(3x-2-1\right)\left[\left(3x-2\right)^2+3x-2+1\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-2\right)^2+3x-2+\dfrac{1}{4}-\dfrac{1}{4}+1\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-2+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\right]=0\left(1\right)\)
mà \(\left(3x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}>0,\forall x\)
\(\left(1\right)\Rightarrow3x-3=0\Rightarrow3x=3\Rightarrow x=1\)
Đúng 2
Bình luận (0)
(\(x-5\))2 = (3 +2\(x\))2 ⇒ \(\left[{}\begin{matrix}x-5=3+2x\\x-5=-3-2x\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=-8\\x=\dfrac{2}{3}\end{matrix}\right.\) vậy \(x\in\){-8; \(\dfrac{2}{3}\)}
27\(x^3\) - 54\(x^2\) + 36\(x\) = 9
27\(x^3\) - 54\(x^2\) + 36\(x\) - 8 = 1
(3\(x\) - 2)3 = 1 ⇒ 3\(x\) - 2 = 1 ⇒ \(x\) = 1
Đúng 2
Bình luận (0)
Xem thêm câu trả lời