Tìm các STN a, b biết tổng của BCNN và ƯCLN của chúng bằng 19.
Cần gấp! Giải rõ ràng nha!!!
1
TÌM 2 STN
a) TỔNG CỦA CHÚNG =432 VÀ ƯCLN =36
b)HIỆU CỦA CHÚNG =84 VÀ ƯCLN=28 BIẾT CHÚNG Ở TRONG KHOẢNG 300 ĐẾN 400
c)TÍCH CỦA CHÚNG =360 VÀ BCNN =60
d)ƯCLN =15 VÀ BCNN GẤP 21000 ƯCLN
GIẢI MÌNH TICK!!
Biết rằng: BCNN(a,b). ƯCLN(a,b)=a.b
a)BCNN của hai số là 600, ƯCLN của chúng nhỏ hơn 10 lần. Số thứ nhất là 120. Tìm số thứ hai
b)ƯCLN của hai số là 12, BCNN của chúng lớn hơn gấp 6 lần ƯCLN. Số thứ nhất là 24. Tìm số thứ hai
c) tổng của hai số là 60, tổng giữa ƯCLN và BCNN là 84. Timd hai số đó
Giải giúp mình nha! ( Làm đc câu nào thì cứ giải ra nhá !)
c)
Gọi 2 số cần tìm là a, b.
BCNN(a, b) = 6.UCLN(a, b) = 6.12 = 72
Ta có BCNN(a, b) . UCLN(a, b) = a.b
Suy ra 72.12 = 24.b ==> b = 36
Vậy 2 số đó là 24 và 36
Tìm số tự nhiên a và b, biết tổng của BCNN với ƯCLN của chúng là 15.Làm đúng và có lời giải,mk tích cho và mk cũng đang cần gấp.
Giả sử a > b
Gọi d = ƯCLN(a,b) (d thuộc N*)
=> a = d.m; b = d.n [(m;n)=1; m > n)
=> BCNN(a;b) = d.m.n
Ta có: BCNN(a;b) + ƯCLN(a;b) = 15
=> d.m.n + d = 15
=> d.(m.n + 1) = 15
=> 15 chia hết cho d
Mà d thuộc N* => d∈{1;3;5;15}d∈{1;3;5;15}
+ Với d = 1 thì m.n + 1 = 15 => m.n = 14
Mà (m;n)=1; m > n => [m=14;n=1m=7;n=2[m=14;n=1m=7;n=2=> [a=14;b=1a=7;b=2[a=14;b=1a=7;b=2
+ Với d = 3 thì m.n + 1 = 5 => m.n = 4
Mà (m;n)=1; m > n => {m=4n=1{m=4n=1=> {a=12b=3{a=12b=3
+ Với d = 5 thì m.n + 1 = 3 => m.n = 2
Mà (m;n)=1; m > n => {m=2n=1{m=2n=1=> {a=10b=5{a=10b=5
+ Với d = 15 thì m.n + 1 = 1 => m.n = 0, vô lý
Vậy các cặp giá trị (a;b) thỏa mãn đề bài là: (14;1) ; (1;14) ; (7;2) ; (2;7) ; (10;5) ; (5;10)
1)Tìm 2 số tự nhiên a và b biết tổng của BCNN và ƯCLN của chúng là 15
2) Tìm hai số tự nhiên a và b biết tổng của BCNN và ƯCLN của chúng là 19
Tìm 2 số , biết rằng BCNN của chúng và ƯCLN của chúng có tổng bằng 19.
Tìm 2 STN biết tổng ƯCLN và BCNN của chúng = 23
Gọi hai số tự nhiên đó là x,y
Vì BCNN (x,y) chia hết cho x ; x chia hết cho UCLN (x,y) nên BCNN (x,y) chia hết cho UCLN (x,y)
Từ đó ta suy ra được BCNN (x,y) + UCLN (x,y) chia hết cho UCLN (x,y) hay 23 chia hết cho UCLN (x,y)
=>UCLN (x,y) thuộc {1,23}
TH1: UCLN(x,y) = 1 thì BCNN= 23-1= 22 và x,y là hai số nguyên tố cùng nhau
=> x.y = 22 = 22.1=1.22=11.2=2.11
Vậy ở trường hợp này( x,y) thuộc {(1,22),(22,1),{11,2),(2,11)}
TH2:Với UCLN (x,y) = 22 thì BCNN (x,y) = 23 - 22=1 (vô lí)
Vậy (x,y) thuộc {(1,22),(22,1),(11,2),(2,11)}
Tìm 2 số biết rằng tự nhiên biết rằng BCNN của chúng và ƯCLN của chúng có tổng bằng 19
Gọi m=BCNN(a;b) => m=ax
Gọi n= UCLN(a;b)=> a=ny
=> m=n(xy) =n.h
mà m+n = 19 => n(1+h)=19
nếu n=19 => h=0 ( vô lí)
Vậy n=1 => m=18
(a;b)=1 và a;b là ước của 18 => 2 số cần tìm là 1;18 hoặc 9;2
Tìm các số tự nhiên a,b biết rằng:
a, Tổng của chúng bằng 84. ƯCLN của chúng bằng 6
b, Tích bằng 300, ƯCLN bằng 5
c, ƯCLN = 10, BCNN = 900
a, Gọi hai số phải tìm là a,b. Ta có (a;b) = 6 => a = 6a’, b = 6b’ với (a’,b’) = 1(a,b,a’,b’ ∈ N)
Do đó: a+b = 84 => 6.(a’+b’) = 84 => a’+b’ = 14
Chọn cặp số a’,b’ là hai số nguyên tố cùng nhau có tổng bằng 14 ta được:
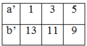
Do đó:
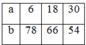
b, Gọi hai số phải tìm là a.b. Ta có (a;b) = 5 => a = 5a’, b = 5b’ với (a’,b’) = 1 (a,b,a’,b’ ∈ N)
Do ab = 300 => 25a’b’ = 300 => a’b’ = 12 = 4.3
Chọn cặp số a’,b’ nguyên tố cùng nhau có tích bằng 12 ta được:
a’ = 1, b’ = 12 => a = 5, b = 60
a’ = 3, b’ = 4 => a = 15, b = 20
c, Gọi hai số phải tìm là a,b. Ta có (a;b) = 10 => a = 10a’; b = 10b’ với (a’,b’) = 1 (a,b,a’,b’ ∈ N, a’<b’). Do đó: ab = 100a’b’ (1)
Mặt khác: ab = [a,b].(a,b) = 900.10 = 9000 (2)
a’ = 1, b’ = 90 => a = 10, b = 900
a’ = 2, b’ = 45 => a = 20, b = 450
a’ = 5, b’ = 18 => a = 50, b = 180
a’ = 9, b’ = 10 => a = 90, b = 100
Bài 1 : Tìm 2 STN a , b biết :
a) Tổng của chúng là 162 và ƯCLN của chúng là 27
b) Chúng nhỏ hơn 200 , hiệu của chúng là 90 và ƯCLN là 15
c) BCNN (a , b) = 300 ; ƯCLN (a , b) = 15
d) a . b = 2940 và BCNN (a , b) = 210
a) Vì ƯCLN ( a , b ) = 27
=> a = 27x , b = 27y , ( x , y ) = 1
Mà a + b = 162
Thay a = 27x , b = 27y vào a + b = 162 ta được
27x + 27 y = 162
27 . ( x + y ) = 162
x + y = 162 : 6
Ta có : 6 = x + y = 1 + 5 = 5 + 1 = 2 + 4 = 4 + 2 = 3 + 3
Mà ( x , y ) = 1 => ( x , y ) = ( 1,5 ) ; ( 5,1 ) ; ( 3 ; 3 )
+ Nếu x = 5 , y = 1 => a = 135,b=27
+ Nếu x = 1 , y = 5 => a = 27 , b = 135
+ Nếu x = 3 , y = 3 => a = 81 , b = 81
Vậy ( a , b ) = ( 135 , 27 ) ; ( 27,135 ) ; ( 81 , 81 )
a) Vì ƯCLN ( a , b ) = 27
=> a = 27x , b = 27y , ( x , y ) = 1
Mà a + b = 162
Thay a = 27x , b = 27y vào a + b = 162 ta được
27x + 27 y = 162
27 . ( x + y ) = 162
x + y = 162 : 6
Ta có : 6 = x + y = 1 + 5 = 5 + 1 = 2 + 4 = 4 + 2 = 3 + 3
Mà ( x , y ) = 1 => ( x , y ) = ( 1,5 ) ; ( 5,1 ) ; ( 3 ; 3 )
+ Nếu x = 5 , y = 1 => a = 135,b=27
+ Nếu x = 1 , y = 5 => a = 27 , b = 135
+ Nếu x = 3 , y = 3 => a = 81 , b = 81
Vậy ( a , b ) = ( 135 , 27 ) ; ( 27,135 ) ; ( 81 , 81 )