Giải phương trình: \(15x-2x^2-5=\sqrt{2x^2-15x+11}\)

Những câu hỏi liên quan
Giải phương trình :
\(2\sqrt{2x-2}+5\sqrt{6x-29}+\sqrt{10-x}+\left(9-x\right)\sqrt{x-8}=x^2-15x+88\)
Nó có 1 nghiệm là 9
Bạn chứng minh nó là nghiệm duy nhất đi
Đúng 0
Bình luận (0)
Giải phương trình:
\(3x^2-x+36=4\sqrt{6x^2-15x+27}+6\sqrt{2x^2+8x-6}\)
Giải phương trình:
a) \(\sqrt{2x^2-15x+26}=x-4\)
\(\left(\sqrt{2x^2-15x+26}\right)\)^2=\(\left(x-4\right)^2\) (ĐKXĐ;x>=4)
\(2x^2\)-15x+26=\(^{x^2-8x+16}\)
\(x^2\)-7x+10=0
\(x^2\)-7x+\(\frac{49}{4}\)=\(\frac{9}{4}\)
(x-\(\frac{7}{4}\))^2=\(\left(\frac{3}{2}\right)^2\)
x-\(\frac{7}{4}\) =\(\frac{3}{2}\)
x=3.25 (khong tm dk)
v...................
Đúng 0
Bình luận (0)
Giải phương trình
\(2x^2-15x+34=3\sqrt[3]{4x-8}\)
Giải phương trình:
\(\left(2x+14\right)\sqrt{x+5}=x^2+15x+38\)
Giúp với
Giải phương trình \(2x^3-15x^2+26x-5=0\)
2x3 - 15x2 + 26x - 5 = 0
<=> 2x3 - 10x2 - 5x2 + 25x + x - 5 = 0
<=> 2x2( x - 5 ) - 5x( x - 5 ) + ( x - 5 ) = 0
<=> ( x - 5 )( 2x2 - 5x + 1 ) = 0
<=> \(\orbr{\begin{cases}x-5=0\\2x^2-5x+1=0\end{cases}}\)
+) x - 5 = 0 <=> x = 5
+) 2x2 - 5x + 1 = 0
Δ = b2 - 4ac = (-5)2 - 4.2.1 = 25 - 8 = 17
Δ > 0, áp dụng công thức nghiệm thu được \(x_1=\frac{5+\sqrt{17}}{4};x_2=\frac{5-\sqrt{17}}{4}\)
Vậy phương trình đã cho có ba nghiệm \(x_1=\frac{5+\sqrt{17}}{4};x_2=\frac{5-\sqrt{17}}{4};x_3=5\)
Giải hệ bất phương trình sau:
15
x
-
2
2
x
+
1
3...
Đọc tiếp
Giải hệ bất phương trình sau: 15 x - 2 > 2 x + 1 3 2 x - 4 < 3 x - 14 2
Tập xác định D = R.
Giải từng bất phương trình:
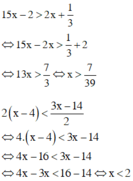
Vậy tập nghiệm của hệ bất phương trình là
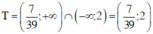
Đúng 0
Bình luận (0)
Giải hệ phương trình sau
\(\hept{\begin{cases}y^2\sqrt{2x-1}+\sqrt{3}\\2y^4\left(5x^2-17x+6\right)=6-15x\end{cases}}=5y^2-\sqrt{6x-3}\)
giải phương trình vô tỉ sau
\(15x^2+2\left(x-1\right)\sqrt{x+2}=2x-5\)
















