Cho hình thoi ABCD có cạnh bằng 2a , ABC=60 độ . Tính độ dài của véc tơ AC .

Những câu hỏi liên quan
Cho hình thoi ABCD có góc BAC=60*, cạnh AB=1. Độ dài của véc tơ AC là bnhiu?
Cho hình chữ nhật ABCD tâm O có cạnh AB=2a,OA=a√5.Tính độ dài véc tơ BC
ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
=>O là trung điểm chung của AC và BD
ABCD là hình chữ nhật
=>AB=CD=2a; BC=AD
O là trung điểm của AC
=>\(AC=2\cdot AO=2a\cdot\sqrt{5}\)
=>\(BD=2a\sqrt{5}\)
ABCD là hình chữ nhật
=>ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC^2=AC^2-AB^2=\left(2a\sqrt{5}\right)^2-\left(2a\right)^2=20a^2-4a^2=16a^2\)
=>BC=4a
=>\(\left|\overrightarrow{BC}\right|=4a\)
Đúng 1
Bình luận (0)
cho hình thoi abcd có cạnh bằng 2cm, góc A bằng 60 độ. Khi đó độ dài đường chéo AC của hình thoi là
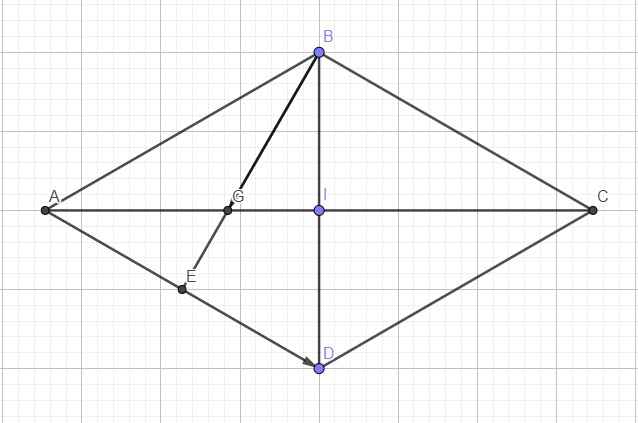
Cho hình thoi ABCD tâm O có cạnh bằng 2a và góc ABC =120 độ. Gọi G là trọng tâm tam giác ABD, tính độ dài của vectơ BG + vectơ AD
Cho hình thoi ABCD tâm O có cạnh bằng 2a và góc ABC =120 độ. Gọi G là trọng tâm tam giác ABD, tính độ dài của vectơ BG + vectơ AD
\(\widehat{ABC}=120^0\Rightarrow\widehat{DAB}=180^0-120^0=60^0\)
\(\Rightarrow\Delta ABD\) đều
Gọi E là trung điểm AD \(\Rightarrow\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BD}+\dfrac{1}{2}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BE}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}+\overrightarrow{AD}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}=\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{4}{3}\overrightarrow{AD}=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\)
Đặt \(\overrightarrow{u}=\overrightarrow{BG}+\overrightarrow{AD}\Rightarrow\left|\overrightarrow{u}\right|^2=\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\right)=\dfrac{4}{9}AB^2+\dfrac{16}{9}AD^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AD}\)
\(=\dfrac{4}{9}.4a^2+\dfrac{16}{9}4a^2-\dfrac{16}{9}.2a.2a.cos60^0=\dfrac{16}{3}a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\dfrac{4a\sqrt{3}}{3}\)
Đúng 2
Bình luận (0)
cho hình chữ nhật ABCD có AB=2a, BC=a\(\sqrt{2}\). Tính độ dài véc tơ\(\overrightarrow{u}=\overrightarrow{AB}-\overrightarrow{BC}\)
\(\left|\overrightarrow{AB}-\overrightarrow{BC}\right|=\left|\overrightarrow{AB}+\overrightarrow{CB}\right|=BD=a\sqrt{6}\)
Đúng 0
Bình luận (0)
cho hình thoi ABCD cạnh bằng a có tâm O, góc BAD =60 ĐỘ. tính độ dài vec tơ sau.
a) VECTO AB + VECTO AD.
b) VECTO AB - VECTO AC.
c)VECTO AB + VECTO AC.
d) VECTO AD + VECTO CB.
e) VECTO OB - VECTO DC
1.Cho hình thoi ABCD có cạnh =a.Biết góc B=60 độ
a)C/m tam giác ABC đều
b)Tính diện tích hình thoi ABCD theo a
2.Cho hình vuông ABCD có độ dài cạnh =a.Điểm M bất kì trên đường thẳng AC.Kẻ ME vuông góc AB tại E và MF vuông góc AC tại F.Tìm vị trí của điểm M trên AC để diện tích tam giác CEF lớn nhất
1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)
Hình thoi ABCD có góc A bằng 60o đường thẳng MN cắt cạnh AB,AC theo thứ tự M,N Biết MB+NB bằng độ dài cạnh hình thoi Tính góc MDN