Cho tam giác ABC cho M,N lần lượt là trung điểm của AB và AC và AM=8cm. Tính BC

Những câu hỏi liên quan
Cho tam giác ABC có BC 16cm ,đường cao AH 8cm. Gọi M và N lần lượt là trung điểm của AB và AC. Tính diện tích của tứ giác MNCB? A. 48
c
m
2
B. 40
c
m
2
C. 54
c
m
2
D. 60
c
m
2
Đọc tiếp
Cho tam giác ABC có BC = 16cm ,đường cao AH = 8cm. Gọi M và N lần lượt là trung điểm của AB và AC. Tính diện tích của tứ giác MNCB?
A. 48 c m 2
B. 40 c m 2
C. 54 c m 2
D. 60 c m 2
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.
Suy ra: MN // BC và
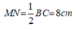
Do đó, tứ giác MNCB là hình thang .
Vì AH = 8cm nên đường cao kẻ từ M đến BC bằng
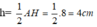
Diện tích hình thang MNCB là :
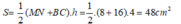
Chọn đáp án A
Đúng 1
Bình luận (0)
cho Tam giác ABC(AB<AC) gọi M,N lần lượt là trung điểm của AB và AC, kẻ NH vuông góc với BC. Tính diện tích tứ giác BMNC biết BC=30cm, NH=8cm
xét tam giác ABC có: N là trug điểm của AC, M là trug điểm của AB => MN là đường trug bình trong tam giác ABC => MN= BC/2=30/2=15cm.diện tích tg BMNC là: (MN+BC)*NH/2 =(15+30)*8/2=180( cm2)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A , có AB =6cm , AC =8cm. Gọi M,N lần lượt là trung điểm của BC , AB.
a/ Chứng minh: ANMC là hình thang vuông
b/ Tính BC , AM
a) Xét tam giác ABC có:
M,N là trung điểm BC,AB
=> MN là đường trung bình
=> MN//AC
=> ANMC là hthang
Mà \(\widehat{NAC}=90^0\)(Tam giác ABC vuông tại A)
=> ANMC là hthang vuông
b) Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét tam giác ABC có:
AM là đường trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right)\)
Đúng 2
Bình luận (0)
cho tam giác ABC có AB<AC.Gọi D là trung điểm BC.Qua D vẽ đgt vuông góc với đgpg của ∠BAC . Đgt đó cắt AB và AC lần lượt là M VÀ N CM BM=CN CHO AC=10cm AB=8cm Tính AM
Cho tam giác ABC có AB=6cm; AC=8cm và A= 90 độ . Gọi I,M,K lần lượt là trung điểm của AB, BC, AC
a) CMR AIMK là hcn và tính diện tích của nó
b) Tính độ dài đoạn AM
c) Gọi P, J, H, S lần lượt là trung điểm
d) Tính điều kiện của tam giác ABC để AIMK là hình vuông
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Gọi M và N lần lượt là trung điểm của AB và AC. Tính MN?
A. 4cm
B. 10cm
C. 5 cm
D. 7cm
Áp dụng định lí Pytago vào tam giác vuông ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
Suy ra: BC = 10cm
Do M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra:
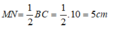
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC = 8cm. Gọi D và E lần lượt là trung điểm các cạnh AB, AC. M và N lần lượt là trung điểm của BD và CE. Khi đó MN =.........cm
Xét tam giác ABC, có:
* D, E lần lượt là trung điểm của AB, AC (gt)
=> DE là đường trung bình của tam giác ABC
=> DE // BC
=> DE = 1/2 BC = 1/2 . 8 = 4 (cm)
Ta có: DE // BC (cmt)
=> DECB là hình thang
Xét hình thang DECB (DE // BC), có:
* M, N lần lượt là trung điểm của DB, EC (gt)
=> MN là đường trung bình của hình thang DECB
=> MN = (DE + BC) : 2 = (4+8) : 2 = 6 (cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC = 8cm. Gọi D và E lần lượt là trung điểm các cạnh AB, AC. M và N lần lượt là trung điểm của BD và CE. Khi đó MN =.........cm
Xét tam giác ABC, có:
* D, E lần lượt là trung điểm của AB, AC (gt)
=> DE là đường trung bình của tam giác ABC
=> DE // BC
=> DE = 1/2 BC = 1/2 . 8 = 4 (cm)
Ta có: DE // BC (cmt)
=> DECB là hình thang
Xét hình thang DECB (DE // BC), có:
* M, N lần lượt là trung điểm của DB, EC (gt)
=> MN là đường trung bình của hình thang DECB
=> MN = (DE + BC) : 2 = (4+8) : 2 = 6 (cm)
nhé !
Đúng 0
Bình luận (0)
cho tam giác ABC, trên tia đối tia AB lấy điểm M sao cho AB=AM. Trên tia AC lấy điểm N sao cho AC=AN. Chứng minh:
a) tam giác ABC=tam giác AMN
b) chứng minh BC//MN
c) gọi P và Q lần lượt là trung điểm của BC và MN. Chứng minh A là trung điểm của PQ
1 cho tam giác abc . m,n lần lượt là trung điểm của bc và ac . am và bn cắt nhau tại o
a, so sánh diện tích abo với bom
b biết om=1cm tính ao
2 cho tam giác abc. m,n,p lần lượt là trung điểm của ab , ac, bc nối mn được tứ giác mnbc có diện tích bằng 180cm2 tính diện tích abc
CHO TAM GIÁC ABC CÀN TẠI A VÀ N LÀ TRUNG ĐIỂM CỦA BC. KẺ MH VÀ MK LẦN LƯỢT VUÔNG GÓC VS AB VÀ AC ( H THUỘC AB, K THUỘC AC)
a)TAM GIÁC AMB=TAM GIÁC MCK
b)CHO BC =8CM . TÍNH ĐỘ DÀI CỦA CẠNH MK,
c)CHO HK=1/2BC.KHI ĐÓ TAM GIÁC ABC LÀ TAM GIÁC GÌ? VÌ SAO?
Sửa đề: M là trung điểm của BC
a) Sửa đề: ΔHBM=ΔKCM
Xét ΔHBM vuông tại H và ΔKCM vuông tại K có
MB=MC(M là trung điểm của BC)
\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
Do đó: ΔHBM=ΔKCM(cạnh huyền-góc nhọn)
Đúng 0
Bình luận (0)


















