Tìm số dư khi chia 1011 cho 3, cho 9. Giải thich vì sao ra đáp án như vậy ?
Những câu hỏi liên quan
67,035 chia cho 54 . đáp án là 1,241. Vì sao số dư lại là 0,021 . Cho mình lài giải chi tiết nhé
vì bạn chưa chia xong, bạn phải thêm 0 để chia thêm. nếu bạn ko chia đc nữa thì phép tính đó có dư
Đúng 1
Bình luận (1)
26 tháng 12 2022 lúc 20:46
The door could not be opened without using force.
=> Only
(Mọi người cho em xin phần giải thích vì sao ra đáp án như vậy với ạ,e cảm ơn nhiều ạ)
Only by using force could the door be open.
Only by + Ving/ Noun + aux + S + V : chỉ bằng cách
CBĐ nói về khả năng trong quá khứ: S + could be + P2 (by O)
Without + Ving / N : mà không có
Đúng 4
Bình luận (3)
Only by using force could the door be opened
Đảo ngữ:
Only by+V-ing/N+trợ V+S+V: Chỉ bằng.........thì.........
Đúng 3
Bình luận (1)
theo quan điểm của mình thì nó là thế này ( chả biết đúng hay sai nx bạn à )
The door could not be opened without using force.
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Một số tự nhiên khi chia cho 3 thì dư 2; chia cho 4 thì dư 1. Vậy số tự nhiên đó khi chia cho 12 thì sẽ có số dư là 5. Đúng ko các bạn Đáp án là 5 phải ko
1.Số tự nhiên a chia cho 60 được số dư là 31, còn khi chia số đó cho 12 được thương là 17. Tìm số a.
Các bạn nhớ giải ra cho mình nha đừng ghi mỗi đáp án
Đáp án bài 2 vòng 14Bài thi số 2: Đi tìm kho báuBiết số 30xy chia hết cho cả 2 và 9 và chia 5 dư 2. Khi đó x + y ... Đáp án: 6 Cho 20 điểm, trong đó có a điểm thẳng hàng (a 20). Cứ qua 2 điểm ta vẽ được một đường thẳng. Tìm a biết vẽ được tất cả 170 đường thẳng. Đáp án: 7Cho AOB 1350. C là một điểm nằm trong AOB biết BOA 900. Số đo AOC là …0. Đáp án: 45Cho tổng S 30 + 32 + 34 + 36 + … + 32002. Khi đó 8S - 32004 - 1 ... Đáp án: -2 Chữ số tận cùng của số 931999 là ... Đáp án: 7 Có tất c...
Đọc tiếp
Đáp án bài 2 vòng 14Bài thi số 2: Đi tìm kho báu
Biết số 30xy chia hết cho cả 2 và 9 và chia 5 dư 2. Khi đó x + y = ... Đáp án: 6
Cho 20 điểm, trong đó có a điểm thẳng hàng (a < 20). Cứ qua 2 điểm ta vẽ được một đường thẳng. Tìm a biết vẽ được tất cả 170 đường thẳng. Đáp án: 7
Cho AOB = 1350. C là một điểm nằm trong AOB biết BOA = 900. Số đo AOC là …0. Đáp án: 45
Cho tổng S = 30 + 32 + 34 + 36 + … + 32002. Khi đó 8S - 32004 - 1 = ... Đáp án: -2
Chữ số tận cùng của số 931999 là ... Đáp án: 7
Có tất cả bao nhiêu số có 3 chữ số chia hết cho 5? Đáp án: 180
Có tất cả bao nhiêu số có 3 chữ số chia hết cho cả 2 và 5? Đáp án: 90
So sánh: 31234 và 21851 ta được 31234 …21851. Điền dấu (>; <; =) thích hợp vào chỗ chấm. Đáp án: >
Số học sinh khối 6 của một trường trong khoảng từ 120 đến 150 học sinh. Khi xếp hàng 12, hàng 18 đều thiếu 1 học sinh. Vậy số học sinh khối 6 của trường đó là … học sinh. Đáp án: 143
Số phần tử của tập hợp A = {1; 3; 5; …; 29; 31} là ... Đáp án: 16
Tập hợp các chữ cái trong cụm từ “VIOLYMPIC VÒNG 14” có số phần tử là ... Đáp án: 10
Tập hợp các số là ước của 75 và là bội của 3 là S = {…}. Đáp án: 3;15;75
Tập hợp các số tự nhiên n để 16 + 7n chia hết cho n + 1 là S = {...}. (Nhập các giá trị theo thứ tự tăng dần, ngăn cách nhau bởi dấu “;”). Đáp án: 0;2;8
Tìm cặp số tự nhiên (x0;y0) thỏa mãn (2x + 1)(y - 5) = 12 sao cho x0 + y0 lớn nhất.
Tìm số 1x8y2 lớn nhất chia hết cho 36. Đáp án: 19872
Tìm số nguyên lớn nhất để n + 2 chia hết cho n - 3. Đáp án: 8
Tìm số tự nhiên a biết 1960 và 2002 chia cho a có cùng số dư là 28. Đáp án: 42
Tìm số tự nhiên a nhỏ nhất thỏa mãn a chia cho 120 dư 58, chia cho 135 dư 88. Đáp án: 898
Tìm số tự nhiên nhỏ nhất, biết rằng khi chia số này cho 29 dư 5 và chia cho 31 dư 28. Đáp án: 121
Tìm số tự nhiên nhỏ nhất chia 18 dư 14, còn chia cho 5 thì dư 2. Đáp án: 32
Tìm số tự nhiên x biết: (1/1.2.3 + 1/2.3.4 + ... + 1/8.9.10)x = 22/45. Đáp án: 2
Tìm tổng của tất cả các số nguyên x thỏa mãn: -2016 ≤ x ≤ 2016. Đáp án: 0
Tìm tổng của tất cả các số tự nhiên có hai chữ số và chia hết cho 9. Đáp án: 585
Tìm x lớn nhất thỏa mãn: 2.ǀx + 9ǀ = 10. Đáp án: -4
Tìm x thỏa mãn: 720 : (x - 17) = 12. Đáp án: 77
Tính: 28.47 + 28.43 + 72.29 + 72.61 = … Đáp án: 9000
Tính: 512.(2 - 128) - 128.(-512) = … Đáp án: 1024
Tính: 4524 - (864 - 999) - (36 + 3999) = … Đáp án: 624
Tổng tất cả các giá trị x thỏa mãn: 3.ǀx - 5ǀ = 21 là ... Đáp án: 10
Biết số 30xy chia hết cho cả 2 và 9 và chia 5 dư 2. Khi đó x + y = ... Đáp án: 6
Cho 20 điểm, trong đó có a điểm thẳng hàng (a < 20). Cứ qua 2 điểm ta vẽ được một đường thẳng. Tìm a biết vẽ được tất cả 170 đường thẳng. Đáp án: 7
Cho AOB = 1350. C là một điểm nằm trong AOB biết BOA = 900. Số đo AOC là …0. Đáp án: 45
Cho tổng S = 30 + 32 + 34 + 36 + … + 32002. Khi đó 8S - 32004 - 1 = ... Đáp án: -2
Chữ số tận cùng của số 931999 là ... Đáp án: 7
Có tất cả bao nhiêu số có 3 chữ số chia hết cho 5? Đáp án: 180
Có tất cả bao nhiêu số có 3 chữ số chia hết cho cả 2 và 5? Đáp án: 90
So sánh: 31234 và 21851 ta được 31234 …21851. Điền dấu (>; <; =) thích hợp vào chỗ chấm. Đáp án: >
Số học sinh khối 6 của một trường trong khoảng từ 120 đến 150 học sinh. Khi xếp hàng 12, hàng 18 đều thiếu 1 học sinh. Vậy số học sinh khối 6 của trường đó là … học sinh. Đáp án: 143
Số phần tử của tập hợp A = {1; 3; 5; …; 29; 31} là ... Đáp án: 16
Tập hợp các chữ cái trong cụm từ “VIOLYMPIC VÒNG 14” có số phần tử là ... Đáp án: 10
Tập hợp các số là ước của 75 và là bội của 3 là S = {…}. Đáp án: 3;15;75
Tập hợp các số tự nhiên n để 16 + 7n chia hết cho n + 1 là S = {...}. (Nhập các giá trị theo thứ tự tăng dần, ngăn cách nhau bởi dấu “;”). Đáp án: 0;2;8
Tìm cặp số tự nhiên (x0;y0) thỏa mãn (2x + 1)(y - 5) = 12 sao cho x0 + y0 lớn nhất.
Tìm số 1x8y2 lớn nhất chia hết cho 36. Đáp án: 19872
Tìm số nguyên lớn nhất để n + 2 chia hết cho n - 3. Đáp án: 8
Tìm số tự nhiên a biết 1960 và 2002 chia cho a có cùng số dư là 28. Đáp án: 42
Tìm số tự nhiên a nhỏ nhất thỏa mãn a chia cho 120 dư 58, chia cho 135 dư 88. Đáp án: 898
Tìm số tự nhiên nhỏ nhất, biết rằng khi chia số này cho 29 dư 5 và chia cho 31 dư 28. Đáp án: 121
Tìm số tự nhiên nhỏ nhất chia 18 dư 14, còn chia cho 5 thì dư 2. Đáp án: 32
Tìm số tự nhiên x biết: (1/1.2.3 + 1/2.3.4 + ... + 1/8.9.10)x = 22/45. Đáp án: 2
Tìm tổng của tất cả các số nguyên x thỏa mãn: -2016 ≤ x ≤ 2016. Đáp án: 0
Tìm tổng của tất cả các số tự nhiên có hai chữ số và chia hết cho 9. Đáp án: 585
Tìm x lớn nhất thỏa mãn: 2.ǀx + 9ǀ = 10. Đáp án: -4
Tìm x thỏa mãn: 720 : (x - 17) = 12. Đáp án: 77
Tính: 28.47 + 28.43 + 72.29 + 72.61 = … Đáp án: 9000
Tính: 512.(2 - 128) - 128.(-512) = … Đáp án: 1024
Tính: 4524 - (864 - 999) - (36 + 3999) = … Đáp án: 624
Tổng tất cả các giá trị x thỏa mãn: 3.ǀx - 5ǀ = 21 là ... Đáp án: 10
- Đây chỉ là đáp án mình giải. Nếu có gì sai sót mong các bạn bỏ qua.
Đúng 1
Bình luận (0)
Số tự nhiên a khi chia cho 5 dư 3, khi chia cho 7 dư 2. Hỏi a chia cho 35 có số dư là bao nhiêu ? ( Giải kĩ cấm ghi nghiêm đáp án )
Theo bài ra ta có :
a : 5 ( dư 3 )
a : 7 ( dư 2 )
=> a + 5 chia hết cho 5 ; 7
Cả 5 và 7 đều là số nguyên tố => a + 5 chia hết cho 5 . 7 = 35
=> a + 5 chia hết cho 35
=> a chia 35 dư 30
Đúng 1
Bình luận (0)
Một số có tổng các chữ số chia cho 9 (cho 3) dư m thì số đó chia cho 9 (cho 3) cũng dư m.
Ví dụ: Số 1543 có tổng các chữ số bằng 1 + 5 + 4 + 3 = 13. Số 13 chia 9 dư 4 chia cho 3 dư 1. Do đó số 1543 chia cho 9 dư 4, chia cho 3 dư 1.
Tìm số dư khi chia mỗi số sau cho 9, cho 3: 1546; 1527; 2468; 1011.
+) 1546 có 1 + 5 + 4 + 6 =16. 16 chia 3 dư 1, chia 9 dư 7.
Do đó 1546 chia 3 dư 1, chia 9 dư 7.
+) 1527 có 1 + 5 + 2 + 7 = 15. Ta thấy 15 chia 9 thư 6 và 15 chia 3 dư 0 nên 1527 chia 9 dư 6, chia hết cho 3.
+) 2468 có 2 + 4 + 6 + 8 = 20. 20 chia 9 dư 2, chia 3 dư 2.
Do đó 2468 chia 3, chia 9 đều dư 2.
+) 
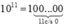có tổng các chữ số bằng 1. 1 chia 3 và 9 đều dư 1.
Do đó 1011 chia 3, chia 9 đều dư 1.
Đúng 0
Bình luận (0)
Chứng tỏ rằng nếu p là số nguyên tố lớn hơn 3 thì p^2-1 chia hết cho 3.
Đáp án: Xét số nguyên tố p khi chai cho 3. Ta có: p=3k+1 hoặc p=3k+2.
Nếu p=3k+1 thì p^2-1=(3k+1)^2-1 =9k^2+6k chia hết cho 3
Nếu p=3k+12 thì p^2-1=(3k+2)^2-1=9k^2+12k chia hết cho 3
Vậy p^2-1 chia hết cho 3.
Mặc dù đã có đáp án như trên nhưng em vẫn không hiểu vì sao có 6k và 12k.
pn lớp mấy vậy
như vậy là pn phải cố hỉu ik chứ
Đúng 0
Bình luận (0)
có 6k và 12k vì khai triển hằng đẳng thức ra:
\(\left(3k+1\right)^2=9k^2+6k+1.\)
tương tự với \(\left(3k+2\right)^2=9k^2+12k+4\)
TH p=3k+2 sai:vì \(\left(3k+2\right)^2-1=9k^2+12k+3\)
+)nếu chưa học về hằng đẳng thức thì có thể nhân ra \(\left(3k+1\right)^2=\left(3k+1\right)\left(3k+1\right)=9k^2+3k+3k+1=9k^2+6k+1\)
còn nếu chưa hiểu thì có thể hiểu
3k+1 chia 3 dư 1=>\(\left(3k+1\right)^2\)chia 3 dư 1=>\(\left(3k+1\right)^2-1⋮3\)
tương tự với Th còn lại
Đúng 0
Bình luận (0)
Ta có
\(\left(3k+1\right)^2=\left(3k+1\right).\left(3k+1\right)-1\)
\(=3k.3k+3k.1+1.3k+1.1-1\)
\(=9k^2+6k+1-1=9k^2+6k\)
Cái dưới cũng tương tự nhé!
Đúng 0
Bình luận (0)
Một số chia hết cho 6 còn dư 4 thì khi chia cho 3 sẽ còn dư mấy? Giải thích vì sao ra số dư đó
Khi chia một số cho 6 mà dư 4 thì chia cho 3 dư 1 vì số nào chia hết cho 6 cũng chia hết cho 3, ta tính sang số dư 4 : 3 = 1(dư 1)
Tớ trước k tớ nhé
Đúng 0
Bình luận (0)