a: 

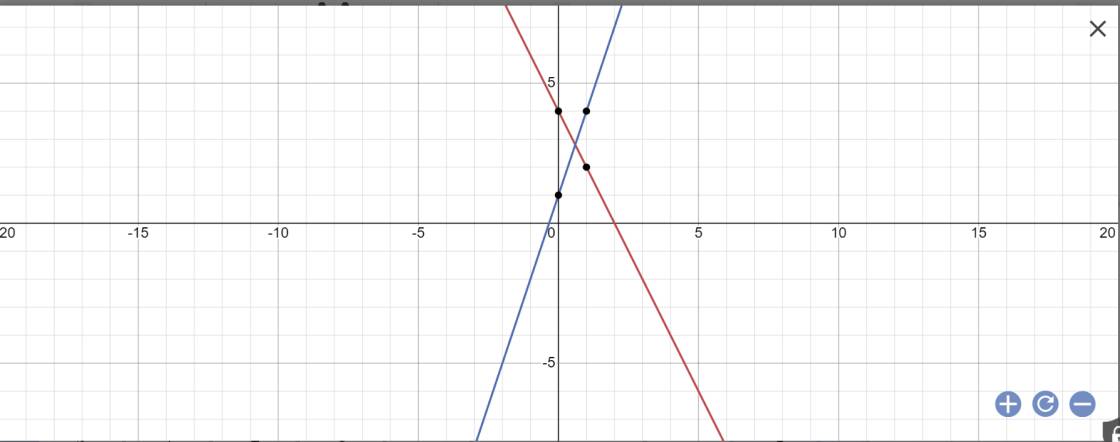
b: Phương trình hoành độ giao điểm là:

4-2x=3x+1

=>-2x-3x=1-4

=>-5x=-3

=>\(x=\dfrac{3}{5}\)

Thay x=3/5 vào y=3x+1, ta được:

\(y=3\cdot\dfrac{3}{5}+1=\dfrac{9}{5}+1=\dfrac{14}{5}\)

Vậy: \(N\left(\dfrac{3}{5};\dfrac{14}{5}\right)\)

c: (d'): y=3x+1

=>a=3

\(tan\alpha=a=3\)

=>\(\alpha\simeq71^034'\)

a: Phương trình hoành độ giao điểm là:

\(3x-2=-\dfrac{2}{3}x\)

=>\(3x+\dfrac{2}{3}x=2\)

=>\(\dfrac{11}{3}x=2\)

=>\(x=2:\dfrac{11}{3}=\dfrac{6}{11}\)

Khi x=6/11 thì \(y=-\dfrac{2}{3}\cdot\dfrac{6}{11}=-\dfrac{4}{11}\)

Vậy: \(A\left(\dfrac{6}{11};-\dfrac{4}{11}\right)\)

b: Đặt (d): y=ax+b

Vì (d)//(d3) nên a=1 và b<>-1

=>(d): y=x+b

Thay x=6/11 và y=-4/11 vào (d), ta được:

\(b+\dfrac{6}{11}=-\dfrac{4}{11}\)

=>\(b=-\dfrac{4}{11}-\dfrac{6}{11}=-\dfrac{10}{11}\)

Vậy: (d): \(y=x-\dfrac{10}{11}\)

b=−411−

b=−411−

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

b: Tọa độ giao điểm là:

\(\left\{{}\begin{matrix}3x-1=-x+2\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{4}\\y=2-\dfrac{3}{4}=\dfrac{5}{4}\end{matrix}\right.\)

Xét phương trình hoành độ giao điểm của 2 đường thẳng (d) và )d'):

        - 3x - 2 = - x + 4. 

<=> - 3x - 2 + x - 4 = 0.

<=> - 2x - 6 = 0.

<=> x = - 3. 

=> y = 7.

Vậy tọa độ giao điểm của hai đường thẳng (d) và (d’) là (-3; 7).

a) Phương trình hoành độ giao điểm của (d₁) và (d₂):

3x - 2 = -2/3 x

⇔ 3x + 2/3 x = 2

⇔ 11/3 x = 2

⇔ x = 2 : 11/3

⇔ x = 6/11

Thay x = 6/11 vào (d₂) ta được:

y = -2/3 . 6/11 = -4/11

Vậy tọa độ giao điểm của (d₁) và (d₂) là A(6/11; -4/11)

b) Gọi (d): y = ax + b

Do (d) // (d₃) nên a = 1

⇒ (d): y = x + b

Do (d) đi qua A(6/11; -4/11) nên thay tọa độ điểm A vào (d) ta có:

6/11 + b = -4/11

⇔ b = -4/11 - 6/11

⇔ b = -10/11

Vậy (d): y = x - 10/11

a.

- Đường thẳng (d) song song với y = 1 - 3x nên ta có:

\(a=-3\)

\(\rightarrow\) Hàm số có dạng \(y=-3x-2\)

- Vẽ đường thẳng \(\left(d\right):y=-3x-2\) 

+ Giao với trục Oy: \(x=0\rightarrow y=-2\Rightarrow A\left(0;-2\right)\)

+ Giao với trục Ox: \(y=0\rightarrow x=-\dfrac{2}{3}\Rightarrow B\left(-\dfrac{2}{3};0\right)\)

Nối 2 điểm A và B ta được đường thẳng (d)

b.

- Gọi tọa độ giao điểm của đường thẳng \(\left(d\right)\) và \(\left(d'\right):y=x+6\) là: \(\left(x_0;y_0\right)\)

- Vì \(\left(x_0;y_0\right)\) thuộc đường thẳng \(\left(d\right)\) nên ta có:

\(y_0=-3x_0-2\) (1)

- Vì \(\left(x_0;y_0\right)\) thuộc đường thẳng \(\left(d'\right):y=x+6\) nên ta có:

\(y_0=x_0+6\) (2)

- Từ (1) và (2), ta có:

\(-3x_0-2=x_0+6\)

\(\Leftrightarrow-3x_0-x_0=6+2\)

\(\Leftrightarrow-4x_0=8\)

\(\Leftrightarrow x_0=-2\)

\(\rightarrow y_0=-2+6=4\)

Vậy tọa độ giao điểm 2 đường thẳng đó là: \(\left(-2;4\right)\)

a,tự vẽ 

b) Xét phương trình hoành độ giao điểm của d và d':
4 - 2x = 3x + 1 
<=> -2x - 3x = 1 - 4
<=> 5x = 3
<=> x = 3/5 
=> y = 14/5