Tìm điểm cực trị của hàm số
y = 2x- giá trị tuyệt đối (x2-4)
Những câu hỏi liên quan
Tìm tất cả các giá trị của m để hàm số
y
1
3
x
3
-
m
x
2
+
m
+
2
x
có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương. A.
m
∈
2...
Đọc tiếp
Tìm tất cả các giá trị của m để hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương.
A. m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
B. m ∈ 2 - 2 7 3 ; 2 + 2 7 3
C. m ∈ - 1 ; 2
D. m ∈ - ∞ ; - 1 ∪ 2 ; + ∞
Để đồ thị hàm số có 2 điểm cực trị thì
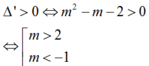
Khi đó, do a = 1 3 > 0 nên hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương . Đồ thị hàm số cắt trục hoành tại 1 điểm duy nhất là x = 0 1 và hai cực trị x 1 ; x 2 x 1 < x 1 thỏa mãn: 0 < x 1 < x 2 2
Ta có:
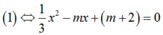
hoặc là vô nghiệm hoặc là có nghiệm kép x = 0
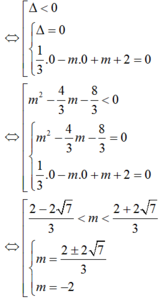
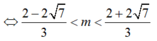
Kết hợp điều kiện ta có:
m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
Chọn: A
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị tham số m để hàm số
y
x
2
+
(
2
-
m
)
x
-
m
+
2
x
+
1
c...
Đọc tiếp
Tìm tất cả các giá trị tham số m để hàm số y = x 2 + ( 2 - m ) x - m + 2 x + 1 có 4 cực trị.
A. - 2 ≤ m ≤ 3 .
B. - 2 < m ≤ 3 .
C. m> 2 hoặc m< -2
D. m> 2 hoặc m< -3
14 tháng 12 2023 lúc 21:35
Tìm các điểm cực trị và các giá trị cực trị của hàm số \(y = \sqrt{2x-x^3}\)
ĐKXĐ: \(2x-x^3>=0\)
=>\(x^3-2x< =0\)
=>\(\left[{}\begin{matrix}x< =-\sqrt{2}\\0< =x< =\sqrt{2}\end{matrix}\right.\)
\(y=\sqrt{2x-x^3}\)
=>\(y'=\dfrac{\left(2x-x^3\right)'}{2\cdot\sqrt{2x-x^3}}=\dfrac{2-3x^2}{2\cdot\sqrt{2x-x^3}}\)
Đặt y'=0
=>\(2-3x^2=0\)
=>\(3x^2=2\)
=>\(x^2=\dfrac{2}{3}\)
=>\(\left[{}\begin{matrix}x=\dfrac{\sqrt{6}}{3}\left(nhận\right)\\x=-\dfrac{\sqrt{6}}{3}\left(loại\right)\end{matrix}\right.\)
Khi \(x=\dfrac{\sqrt{6}}{3}\) thì \(y=\sqrt{2\cdot\dfrac{\sqrt{6}}{3}-\left(\dfrac{\sqrt{6}}{3}\right)^3}\)
\(=\sqrt{\dfrac{4\sqrt{6}}{9}}=\dfrac{2}{3}\cdot\sqrt{\sqrt{6}}\)
Đúng 2
Bình luận (1)
Cho hàm số
y
-
x
2
+
2
x
+
c
x
-
3
có giá trị cực tiểu là m và giá trị cực đại là M. Có bao nhiêu giá trị nguyên của c để m-M4 A. 1 B. 2 C. 4 D. 3
Đọc tiếp
Cho hàm số y = - x 2 + 2 x + c x - 3 có giá trị cực tiểu là m và giá trị cực đại là M. Có bao nhiêu giá trị nguyên của c để m-M=4
A. 1
B. 2
C. 4
D. 3
Cho hàm số yf(x) có đạo hàm f’(x)(x-1)2(x2-2x) với mọi
x
∈
R
. Có bao nhiêu giá trị nguyên dương của tham số m để hàm yf(x2-8x+m) có 5 điểm cực trị A. 15 B. 17 C. 18 D. 16
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f’(x)=(x-1)2(x2-2x) với mọi x ∈ R . Có bao nhiêu giá trị nguyên dương của tham số m để hàm y=f(x2-8x+m) có 5 điểm cực trị
A. 15
B. 17
C. 18
D. 16
Cho hàm số yf(x) có đạo hàm
f
(
x
)
(
x
-
1
)
2
(
x
2
-
2
x
)
, với mọi
x
∈
R
. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x 2 - 2 x ) , với mọi x ∈ R . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x 2 - 8 x + m ) có 5 điểm cực trị?
A. 16
B. 18
C. 17
D. 15
Cho hàm số yf(x) có đạo hàm
f
(
x
)
(
x
-
1
)
2
(
x
2
-
2
x
)
với mọi x thuộc R. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
y
f
(
x
2
-...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x 2 - 2 x ) với mọi x thuộc R. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x 2 - 8 x + m ) có 5 điểm cực trị?
A. 15
B. 17
C. 16.
D. 18
14 tháng 1 2022 lúc 20:33
tìm x và y biết giá trị tuyệt đối của 2x+1+ với giá trị tuyệt đối của y-1 =4
Cho hàm số: yx-3-3(m+1)x2+9x+m-2 (1) có đồ thị là (Cm). Có bao nhiêu giá trị nguyên của tham số m để (Cm) có điểm cực đại, cực tiểu đối xứng với nhau qua đường thẳng y1/2x ? A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Cho hàm số: y=x-3-3(m+1)x2+9x+m-2 (1) có đồ thị là (Cm). Có bao nhiêu giá trị nguyên của tham số m để (Cm) có điểm cực đại, cực tiểu đối xứng với nhau qua đường thẳng y=1/2x ?
A. 0
B. 1
C. 2
D. 3
Tìm min của hàm số : y=giá trị tuyệt đối của (x+1) + căn của (x^2-2x+5)