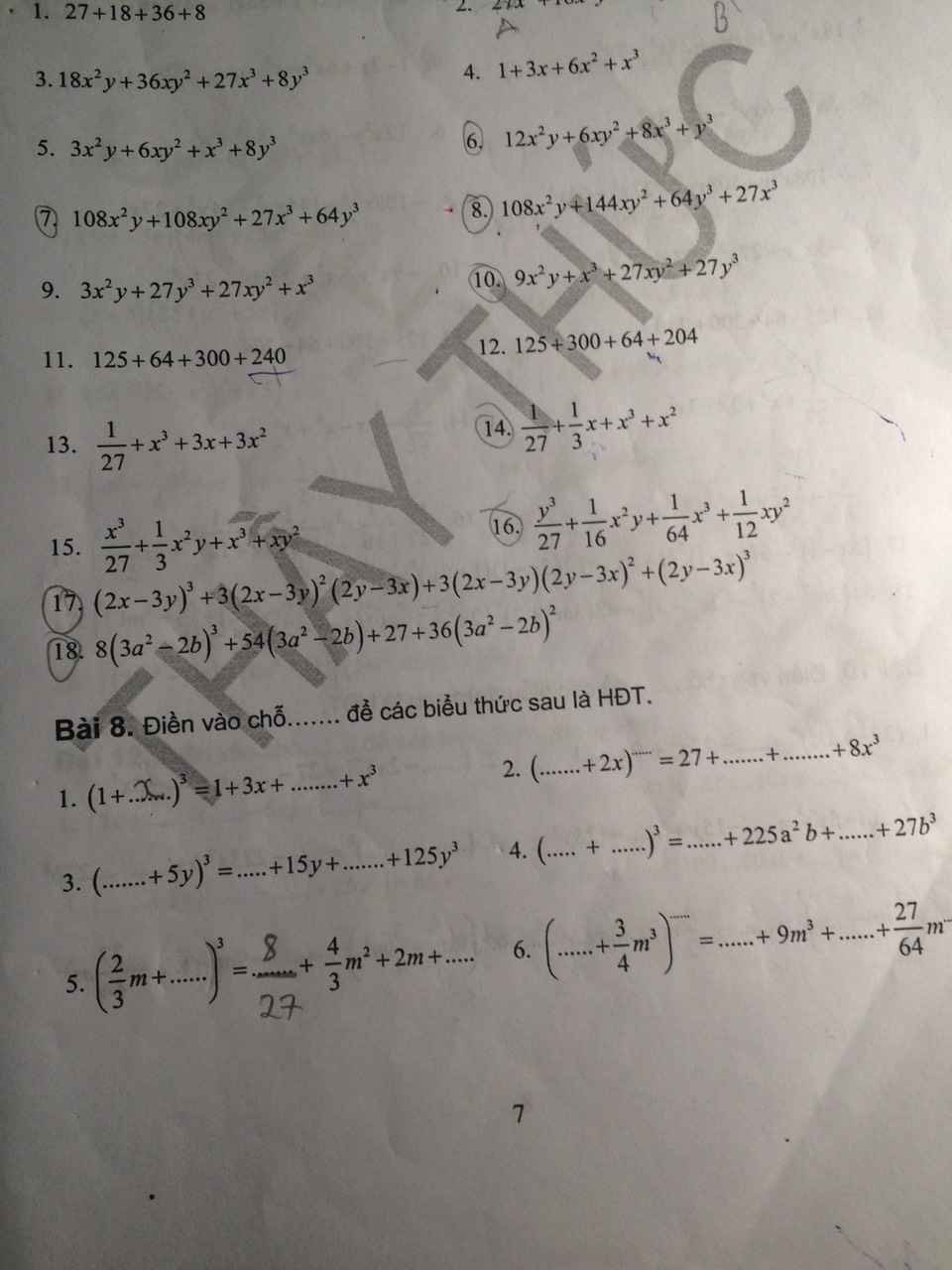
6) Ta có: \(12x^2y+6xy^2+8x^3+y^3\)

\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2+y^3\)

\(=\left(2x+y\right)^3\)

8) Ta có: \(108x^2y+144xy^2+64y^3+27x^3\)

\(=\left(4y\right)^3+3\cdot\left(4y\right)^2\cdot3x+3\cdot4y\cdot\left(3x\right)^2+\left(3x\right)^3\)

\(=\left(4y+3x\right)^3\)

https://www.youtube.com/watch?v=f99DLXfQqOA

Dễ thuộc =))))

Dễ lắm( -.-)

Đầu tiên học 3 hằng đẳng thức viết vào tập khoảng 4,5 lần nếu thuộc rồi thì chuyển qua 3 cái khác đến hết 7 hằng đẳng thức thì xong:-)

Với ba hằng đẳng thức thứ nhất, thứ hai và thứ ba thì rất dễ thuộc (đúng không)

\(\left(a+b\right)^2=a^2+2ab+b^2\)

\(\left(a-b\right)^2=a^2-2ab+b^2\)

\(a^2-b^2=\left(a-b\right)\left(a+b\right)\)

Với hằng đẳng thức thứ tư: \(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)

Bạn hãy ghi nhớ rằng: Số mũ của a sẽ giảm dần từ bậc 3 xuống còn bậc 0; còn số mũ của b sẽ tăng lên từ bậc 0 đến bậc 3.

Với hằng đẳng thức thứ năm: \(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)

Tương tự như hẳng đẳng thức thứ 5; và các dâu của hằng đẳng thức này là " - " và " + " xen kẽ với nhau (đúng không nào)

Với hằng đẳng thức thứ sáu và thứ bảy: \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)

                                                           \(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)

Khi phân tích thành nhân tử, chúng luôn chứa các thừa số: a;b;a^2;ab và b^2

Với hai số a và b đầu tiên; có thể dễ dàng nhận thấy là dấu của chúng phụ thuộc vào lập phương mà chúng phân tích là tổng hay hiệu.

Nếu là (a + b) thì phần sau sẽ là - ab

Nếu là (a - b) thì phần sau sẽ là + ab

x^2 + y^2 = (x + y +\(\sqrt{2xy}\))(x + y - \(\sqrt{2xy}\))

 các bn tk mk nha .mk cảm ơn nhiều

\(a^{2k}-b^{2k}=\left(a+b\right)\left(a^{2k-1}-a^{2k-2}b+a^{2k-3}b^2-....-a^2b^{2k-3}+ab^{2k-2}-b^{2k-1}\right)\)

Tam giác pascal:                                                 1

                                                                     1    2    1

                                                                 1    3       3     1

                                                             1     4      6       4     1

tui ko bt mà cx cm ơn tui à 

kaka keke~~ Dễ xương lawms~ Triệu ....

Vd : \(x^2+6x+10\)

Ta có : 10 không căn được 

Mà : \(x^2+2.x.3+3^2\)

Nhưng 3² chỉ là 9 nên ta cộng thêm 1 ở vế sau 

\(\left(x^2+2.x.3+3^2\right)+1\)

\(\left(x+3\right)^2+1\)

Dư 1 ở ngoài : 

Vì \(\left(x+3\right)^2\ge0\)

=> \(\left(x+3\right)^2+1\ge1\)

=> GTNN  là 1 

Khi ( x + 3 ) = 0

         x = -3

Khi 

Giải

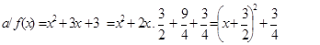
Ta có 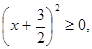 nên  

Vậy: f(x) đạt GTNN bằng  khi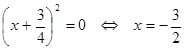 

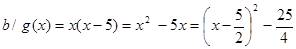
Ta có   nên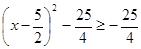 

Vậy: g(x) đạt GTNN bằng  khi 

Có mình 

có mình.

em chưa