Cho hình vẽ , biết AB \(\perp\) AC . Góc EBA = 50o , góc C = 40o
Chứng minh rằng :
a. AD // CM
b. AD // BE
Cho hình vẽ, biết \(\widehat{F}\) = 50o , \(sđ\stackrel\frown{AB}\) = 40o . Chứng minh \(AD\perp BC\)
cho hình vẽ biết AB⊥AC, DAC=130o;B=50o;C=40o. Chứng minh
a.AD//CF
b.AD//BE
Cho AB // EG và một điểm C bất kì như hình vẽ và A = 40o ; E = 50o. Chứng minh rằng AC vuông góc với CE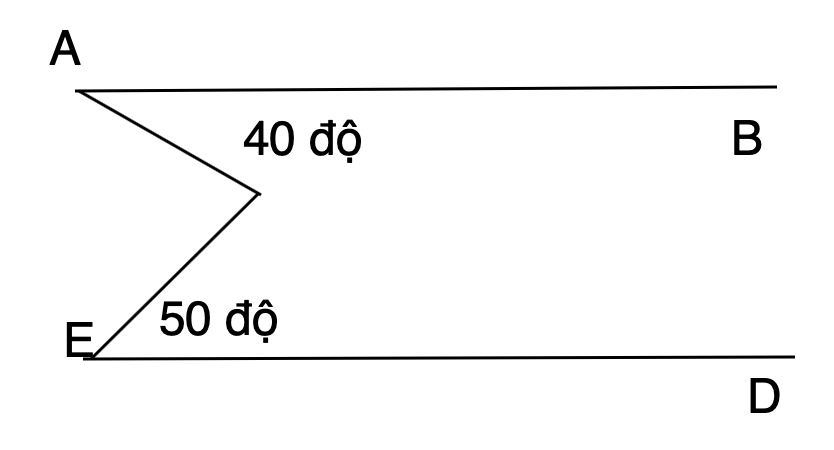
Kẻ 1 đường thẳng t qua C song song với AB và ED.
=> \(\widehat{tCA}=\widehat{A}=40^o\) (so le trong)
\(\widehat{tCE}=\widehat{E}=50^o\) (so le trong)
Ta có: \(\widehat{C}=40^o+50^o=90^o\)
=> \(AC\perp CE\)
Cho tam giác ABC, góc B tù. Từ trung điểm M của BC vẽ đường vuông góc với tia phân giác của góc A tại D, đường này cắt tia AB tại E và tia AC tại F. Từ M vẽ MI vuông góc với AB, MH vuông góc với AC, đường MH cắt tia AD tại N
a) chứng minh BE = CF
b) CM : ME là phân giác góc IMN
c) Tia phân giác góc IMN cắt AC tại K. Chứng minh MK//AD
d) CM : góc MKC = góc EMN
e) Cho góc BAC = 60 độ, AB = c, AC = b. Tính AE, BE AD theo b,c
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE
a) Chứng minh rằng BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng góc A = 50o.
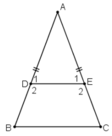
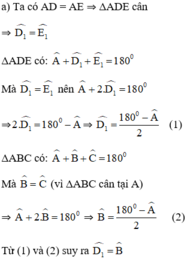
Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
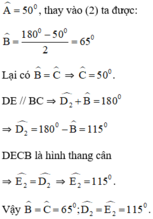
Cho tam giác ABC có 3 góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và AB (D khác phía C đối với AB), vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phỉa B đối với AC). Chứng minh rằng :
a) \(DC=BE\)
b) \(DC\perp BE\)
Cho \(\Delta ABC\)có góc A nhọn và AB=AC. Tia phân giác của góc A cắt BC ở D.
a) Chứng minh AD là trung trực của BC.
b) Vẽ \(BE\perp AC\)tại E, BE cắt AD tại I. Trên tia AB lấy điểm F sao cho AF=AE. Chứng minh \(IF\perp AB\).
c) Chứng minh C,I,F thẳng hàng.
Hình bình hành ABCD có AD = 12cm; AB = 8cm. Từ C vẽ CE vuông góc với AB tại E , CF vuông góc với AD tại F và vẽ BH vuông góc với AC tại H. Nối E với D, cắt BC tại I. Biết BI = 7cm; EI = 8,5cm:
a) Tính độ dài BE, ED.
b) Chứng minh ∆ABH đồng dạng ∆ACE và ∆BHC đồng dạng ∆CFA
c) Chứng minh AC2 = AB.AE + AD. AF
b: Xét ΔAHB vuông tại H và ΔACE vuông tại E có
góc A chung
=>ΔABH đồng dạng với ΔACE
Xét ΔBHC vuông tại H và ΔCFA vuông tại F có
góc BCA=góc CAF
=>ΔBHC đồng dạng với ΔCFA
c: AB/AC=AH/AE
=>AB*AE=AH*AC
BC/AC=CH/AF=BH/CF
=>DA/AC=CH*AF
=>AC*CH=AD*AF
=>AC^2=AB*AE+AD*AF
Cho tam giác ABC. Vẽ đoạn thẳng AD vuông góc AB (D và C nằm khác phía với AB), AD = AB. Vẽ đoạn thẳng AE vuông góc với AC (E và B nằm khác phía với AC), AE = AC.
a, Cho DE = BC.Tính góc ABC
b, Cho góc A không bằng 90 độ. Chứng minh rằng DC=BE
Cho tam giác nhọc ABC . qua A vẽ AH vuông góc BC(Hthuộc Bc).Từ H vẽ HKvuông góc AC ( Kthuộc AC). Qua K vẽ Đường ThẳnG sog sog BC cắt AB tại E
a) Hãy chỉ ra các cặp góc bằng nhau trên hình vẽ? giải thích?
b)Chứng minh AHvuông góc Ek
c)Qua A vẽ AD vuông góc AB sao cho AD=AB Và vẽ AE vuông góc AC sao cho AE=AC( không chứa Bvà C). chứng minh BE=DC