Trong ngũ giác lồi ABCDE, người ta nối trung điểm M của cạnh AB với trung điểm P của cạnh CD, nối trung điểm N của cạnh BC với trung điểm R của cạnh DE. Gọi H và K lần lượt là trung điểm của MP và NR.
Chứng minh HK \\ AE và HK = \(\dfrac{1}{4}\)AE.
Những câu hỏi liên quan
Trong ngũ giác lồi ABCDE, người ta nối trung điểm M của cạnh AB với trung điểm P của cạnh CD, nối trung điểm N của cạnh BC với trụng điểm R của cạnh DE. Gọi H và K lầm lượt là trung điểm của MP và NR. Chứng minh HK song song với AE và HK = \(\frac{1}{4}\)AE.
Giả sử M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, EA của ngụ giác lồi ABCDE. Gọi I, K lần lượt là trung điểm của MP, NQ. Chứng minh rằng: IK = \(\frac{1}{4}\)ED
16 tháng 7 2018 lúc 19:26
Cho ngũ giác lồi ABCDE có M; N; P; Q; R lần lượt là trung điểm của AB; BC; CD; DE; EA. Lấy S; X; Y; Z; T theo thứ tự là trung điểm của NR; MQ; NQ; MP; PR.
a) Hãy tìm tỉ số chu vi và tỉ số diện tích giữa 2 ngũ giác ABCDE và XTYZS ?
b) Tìm điều kiện của ngũ giác ABCDE để ngũ giác XTYZS là ngũ giác đều ? (By: 黒川猫）
Cho ngũ giác đều ABCDE có chiều dài cạnh \(a=\sqrt{17}\)gọi M, N, P , Q theo thứ tự là các trung điểm của AB, BC, DE, AE. Gọi I là trung điểm của NQ, K là trung điểm của MP . Tính IK
.cho ngũ giác lồi ABCDE.M,P,N,R lần lượt là trung điểm của AB,CD,BC,ED.H,K lần lượt là trung điểm của MP,NR.
a.L là trung điểm của BE.Chứng minh K là trung điểm của PL
b.Chứng minh [tex]HK//AE[/tex] ; [tex]HK=\frac{1}{4}AE[/tex]
Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
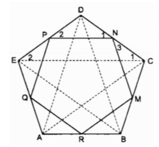
Xét △ ABC và △ BCD:
AB = BC (gt)
∠ B = ∠ C (gt)
BC = CD (gt)
Do đó: △ ABC = △ BCD (c.g.c)
⇒ AC = BD (1)
Xét △ BCD và △ CDE:
BC = CD (gt)
∠ C = ∠ D (gt)
CD = DE (gt)
Do đó: △ BCD = △ CDE (c.g.c) ⇒ BD = CE (2)
Xét △ CDE và △ DEA:
CD = DE (gt)
∠ D = ∠ E (gt)
DE = EA (gt)
Do đó: △ CDE = △ DEA (c.g.c) ⇒ CE = DA (3)
Xét △ DEA và △ EAB:
DE = EA (gt)
∠ E = ∠ A (gt)
EA = AB (gt)
Do đó: △ DEA = △ EAB (c.g.c) ⇒ DA = EB (4)
Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB
Trong △ ABC ta có RM là đường trung bình
⇒ RM = 1/2 AC (tính chất đường trung bình của tam giác)
Mặt khác, ta có: Trong Δ BCD ta có MN là đường trung bình
⇒ MN = 1/2 BD (tính chất đường trung bình của tam giác)
Trong △ CDE ta có NP là đường trung bình
⇒ NP = 1/2 CE (tính chất đường trung bình của tam giác)
Trong △ DEA ta có PQ là đường trung bình
⇒ PQ = 1/2 DA (tính chất đường trung bình của tam giác)
Trong △ EAB ta có QR là đường trung bình
⇒ QR = 1/2 EB (tính chất đường trung bình của tam giác)
Suy ra: MN = NP = PQ = QR = RM
Ta có: ∠ A = ∠ B = ∠ C = ∠ D = ∠ E = ((5-2 ). 180 0 )/5 = 108 0
△ DPN cân tại D
⇒ ∠ (DPN) = ∠ (DNP) = ( 180 0 - ∠ D )/2 = ( 180 0 - 108 0 )/2 = 36 0
△ CNM cân tại C
⇒ ∠ (CNM) = ∠ (CMN) = ( 180 0 - ∠ D )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (ADN) + ∠ (PNM) + ∠ (CNM) = 180 0
⇒ ∠ (PNM) = 180 0 - ( ∠ (ADN) + ∠ (CNM) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ BMR cân tại B
⇒ ∠ (BMR) = ∠ (BRM) = ( 180 0 - ∠ B )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (CMN) + ∠ (BRM) + ∠ (BMR) = 180 0
⇒ ∠ (NMR) = 180 0 - ( ∠ (CMN) + ∠ (BMR) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ ARQ cân tại A
⇒ ∠ (ARQ) = ∠ (AQR) = ( 180 0 - ∠ A )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (BRM) + ∠ (MRQ) + ∠ (ARQ) = 180 0
⇒ ∠ (MRQ) = 180 0 - ( ∠ (BRM) + ∠ (ARQ) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ QEP cân tại E
⇒ ∠ (EQP) = ∠ (EPQ) = ( 180 0 - ∠ E )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (AQR) + ∠ (RQP) + ∠ (EQP) = 180 0
⇒ ∠ (RQP) = 180 0 - ( ∠ (AQR) + ∠ (EQP) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
∠ (EQP) + ∠ (QPN) + ∠ (DPN) = 180 0
⇒ ∠ (QPN) = 180 0 - ( ∠ (EPQ) + ∠ (DPN) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
Suy ra : ∠ (PNM) = ∠ (NMR) = ∠ (MRQ) = ∠ (RQP) = ∠ (QPN)
Vậy MNPQR là ngũ giác đều.
Đúng 0
Bình luận (0)
Cho ngũ giác ABCDE.Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB,BC,DE,EA; H ,K là trung điểm của NQ,MP. CMR: KH//CD.
1.Số đo các góc trong của một đa giác n cạnh lập thành một dãy số cộng biết góc nhỏ nhất là 110 độ,góc lớn nhất là 160 độ.Tìm n2.cho ngũ giác lồi ABCDE.M,P,N,R lần lượt là trung điểm của AB,CD,BC,ED.H,K lần lượt là trung điểm của MP,NR. a.L là trung điểm của BE.Chứng minh K là trung điểm của PLb.Chứng minh HK//AEHK//AE ; HK14AEHK14AE3.Tam giác ABC,trên cạnh AB lấy E sao cho AE13BEAE13BE .Trên cạnh BC lấy F sao cho BF4FC.AF cắt CE tại Da.Chứng minh Diện tích ACFDiện tích AEFb.H,K lần lượt là châ...
Đọc tiếp
1.Số đo các góc trong của một đa giác n cạnh lập thành một dãy số cộng biết góc nhỏ nhất là 110 độ,góc lớn nhất là 160 độ.Tìm n
2.cho ngũ giác lồi ABCDE.M,P,N,R lần lượt là trung điểm của AB,CD,BC,ED.H,K lần lượt là trung điểm của MP,NR. a.L là trung điểm của BE.Chứng minh K là trung điểm của PL
b.Chứng minh HK//AEHK//AE ; HK=14AEHK=14AE
3.Tam giác ABC,trên cạnh AB lấy E sao cho AE=13BEAE=13BE .Trên cạnh BC lấy F sao cho BF=4FC.AF cắt CE tại D
a.Chứng minh Diện tích ACF=Diện tích AEF
b.H,K lần lượt là chân đường vuông góc kẻ từ E,C đến A,F.Chứng minh EH=CK
c.Chứng minh CD=DE
d.Chứng minh diện tích ABC=2.diện tích ABD
Cho hình vuông ABCD. Gọi I, K theo thứ tự là trung điểm của các cạnh AB, CD. Nối CI, AK. CMR: a) Tứ giác AICK là hình bình hành. b) Gọi M là trung điểm của BC. Gọi P, Q lần lượt là giao điểm của DM với IC và AK. CMR: DM = AK và DM vuông AK
a: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành
Đúng 0
Bình luận (0)