Cho tứ giác ABCD có M , N , P thứ tự là trung điểm của AD , AC , BC . Chứng minh tam giác MNP cân

Những câu hỏi liên quan
Cho tứ giác ABCD có AD = BC . M , N , P thứ tự là trung điểm AB , AC và CD . Chứng minh tam giác MNP cân
Tam giác BAC có M A = MB ( M là trung điểm )
NA = NC ( N là tđ )
=> MN là đg tb => MN = 1/2 BC (1)
CMTT NP là đường tb của tam giác ADC => NP = 1/2 AD (2)
AD = BC ( GT ) (3)
Từ (1) (2) (3) => MN = NP
=> tam giác MNP cân tại N
Đúng 0
Bình luận (0)
cho tứ giác ABCD có AD = BC gọi E và F là trung điểm của BD và AC, EF cắt AD , BC ở M và N , H là giao điểm A và BC . Chứng minh tam giác HMN cân
tứ giác ABCD có AD = BC, ác tia DA và CB cắt nhau tại O. Gọi i, k thứ tự là trung điểm của BD và AC. Đường thẳng IK cắt AD, BC theo thứ tự ở E và F. Chứng minh OEF là tam giác cân
Trả lời:
Bạn tham khảo ạ !
Hok tốt
bạn xem ký đầu bài hộ mình
Cho tứ giác ABCD có AD=BC, các tia DA va BC cắt nhau tại O. Gọi I, K lần lượt là trung điểm BD, AC. Đường thẳng IK cắt AD, BC theo thứ tự ở E và F. Chứng minh: tam giác OEF cân
Bài 1: Cho tam giác ABC nhọn ( AB BC ) , đường cao AH. Gọi I , K , M , N theo thứ tự là trung điểm của AB, AC, HC, HB. Chứng minh:a) Tứ giác BCKI là hình thang ?b) IMNKBài 2 : Cho hình bình hành ABCD , có AD vuông góc với AC. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh:a) Tứ giác ADNM là hình bình hành ?b) Tứ giác AMND là hình thoi ?Bài 3 : Cho hình chữ nhật ABCD , P và Q lần lượt là trung điểm của BC và AD. Gọi M là giao điểm của AP và BQ , N là giao điểm của CQ và DP. Chứng minh:a)...
Đọc tiếp
Bài 1: Cho tam giác ABC nhọn ( AB < BC ) , đường cao AH. Gọi I , K , M , N theo thứ tự là trung điểm của AB, AC, HC, HB. Chứng minh:
a) Tứ giác BCKI là hình thang ?
b) IM=NK
Bài 2 : Cho hình bình hành ABCD , có AD vuông góc với AC. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh:
a) Tứ giác ADNM là hình bình hành ?
b) Tứ giác AMND là hình thoi ?
Bài 3 : Cho hình chữ nhật ABCD , P và Q lần lượt là trung điểm của BC và AD. Gọi M là giao điểm của AP và BQ , N là giao điểm của CQ và DP. Chứng minh:
a) Tứ giác APCQ , BPDQ là hình bình hành
b) Tứ giác ABPQ , CDQP là hình chữ nhật
c) Tứ giác MPNQ là hình thoi
d) Tứ giác AMND , BCNM là hình thang cân
MỌI NGƯỜI GIÚP MÌNH TRONG HÔM NAY VỚI Ạ !!! MAI MÌNH KIỂM TRA RÙI !!! THANK KIU EVERYONE, MONG NHẬN ĐK CÂU TRẢ LỜI SỚM ( MÀ MỌI NGƯỜI KHÔNG CẦN VX HÌNH ĐÂU Ạ ^^)
Đúng 0
Bình luận (0)
1) a. xét trong tam giác ABC có
I trung điểm AB và K trung điểm AC =>IK là đường trung bình của tam giác ABC=>IK song song với BC
vậy BCKI là hình thang (vì có hai cạng đáy song song)
b.
IK // và =1/2BC (cm ở câu a) =>IK song song NM
M trung điểm HC và N trung điểm HB mà HB+HC=CB =>MN=IK=1/2BC
suy ra MKIN là hbh => có hai đường chéo bằng nhau =>IM=NK
Đúng 0
Bình luận (0)
Bài 4: Cho tứ giác ABCD(AB//CD). Gọi E;F;K theo thứ tự là trung điểm của AD;BC;AC.
1) So sánh các độ dài của tam giác MIK
2) Chứng minh EF=AB+CD/2
Bài 5: Cho tam giác ABC có D là trung điểm của AB.Tia Dz//BC cắt AC tại E. chứng minh E là trung điểm của AC
Bài 5:
Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
Bài 4:
2: Xét hình thang ABCD có
E,F lần lượt là trung điểm của AD,BC
=>EF là đường trung bình của hình thang ABCD
=>EF//AB//CD và \(EF=\dfrac{AB+CD}{2}\)
Đúng 1
Bình luận (0)
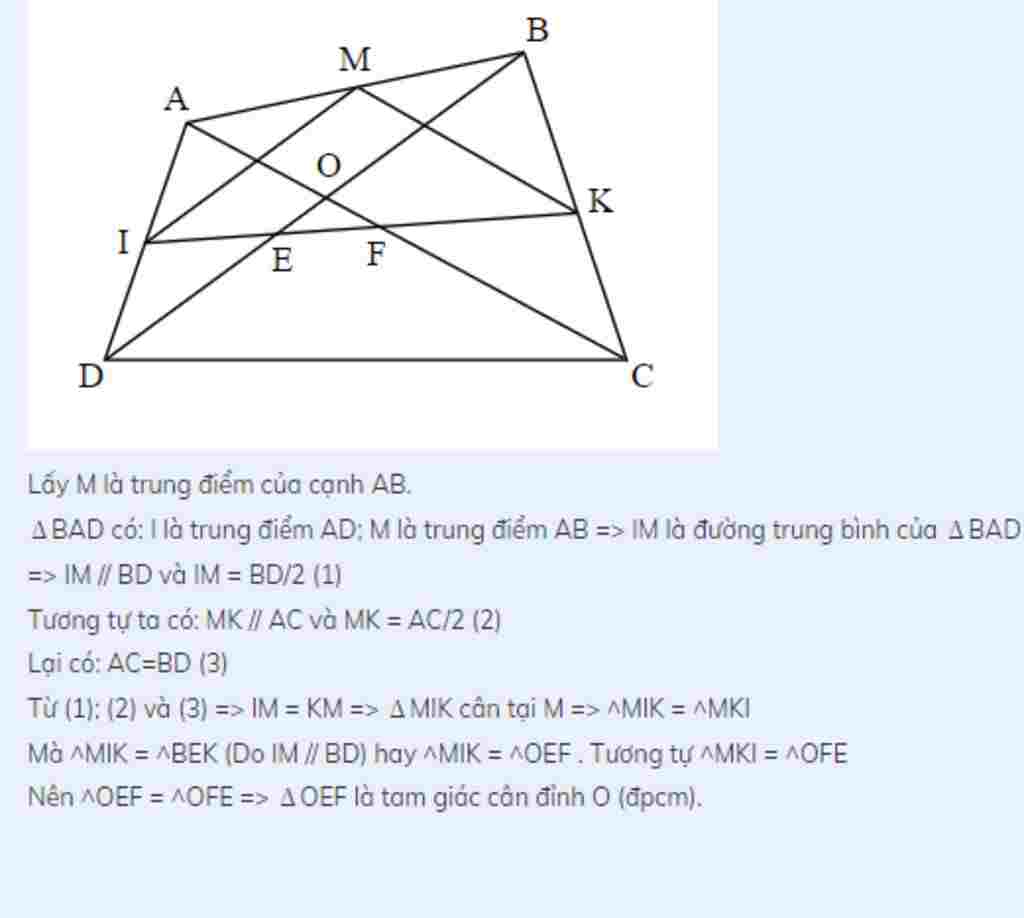
tứ giác ABCD có 2 đường chéo bằng nhau và cắt nhau tại O. Gọi I, K theo thứ tự là trung điểm của AD, BC đường thẳng IK cắt BD, Ac theo thứ tự ở E và F. chứng minh OEF là tam giác cân
Đây là hình của bài
nhưng mik ko chắc đúng
vì mik mới học lớp 7
thông cảm nha
Đúng 0
Bình luận (0)
tứ giác ABCD có 2 đường chéo bằng nhau và cắt nhau tại O. Gọi I, K theo thứ tự là trung điểm của AD, BC đường thẳng IK cắt BD, Ac theo thứ tự ở E và F. chứng minh OEF là tam giác cân
Lấy M là trung điểm của cạnh AB.
\(\Delta\)BAD có: I là trung điểm AD; M là trung điểm AB => IM là đường trung bình của \(\Delta\)BAD
=> IM // BD và IM = BD/2 (1)
Tương tự ta có: MK // AC và MK = AC/2 (2)
Lại có: AC=BD (3)
Từ (1); (2) và (3) => IM = KM => \(\Delta\)MIK cân tại M => ^MIK = ^MKI
Mà ^MIK = ^BEK (Do IM // BD) hay ^MIK = ^OEF . Tương tự ^MKI = ^OFE
Nên ^OEF = ^OFE => \(\Delta\)OEF là tam giác cân đỉnh O (đpcm).
Đúng 0
Bình luận (0)
Tứ giác ABCD có AD=BC, các tia DA và CB cắt nhau tại O. Gọi I, K theo thứ tự là trung điểm của BD, AC. Đường thẳng IK cắt AD và BC theo thứ tự ở E, F. Chứng minh rằng tam giác OEF cân.
Xin cảm ơn ạ.

















