Cho đường tròn (O) và một điểm M cố định không nẳm trên đường tròn. Qua M vẽ một cát tuyến bất kì cắt đường tròn ở A và B.
Chứng minh rằng tích MA.MB không đổi ?
Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn .Qua M vẽ một cát tuyến bất kì cắt đường tròn ở A và B.Chứng minh rằng tích MA.MB không đổi
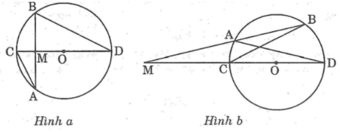
*Trường hợp M nằm bên trong đường tròn (O) (hình a)
Kẻ cát tuyến AB đi qua M và đường thẳng MO cắt đường trong tại C và D
Xét hai tam giác MBD và MCA ta có:

Ta có điểm M và O cố định ,suy ra điểm C và D cố định .Do vậy độ dài các đoạn MC và MD không đổi, suy ra tích MC.MD không đổi
Do tích MC.MD không đổi nên kết hợp với (*) suy ra tích MA.MB cũng không đổi khi cát tuyến AB thay đổi
*Trường hợp M nằm bên ngoài đường tròn (O) (hình b)
Kẻ cát tuyến MAB bất kì của (O) và đường thẳng MO cắt đường tròn tại C và D
Xét hai tam giác MCB và MAD ta có:

Ta có điểm M và O cố định ,suy ra điểm C và D cố định .Do vậy độ dài các đoạn MC và MD không đổi, suy ra tích MC.MD không đổi
Do tích MC.MD không đổi nên kết hợp với (**) suy ra tích MA.MB cũng không đổi khi cát tuyến AB thay đổi
Cho đường tròn (O) một điểm M cố định không nằm trên đường tròn, qua M kẻ cát tuyến cắt (O) tại A và B. CMR tích MA.MB không đổi
Giải
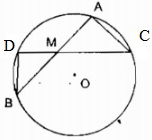
Trường hợp M ở bên trong đường tròn (O)
Kẻ cát tuyến AB bất kỳ và kẻ đường thẳng MO cắt đường tròn tại C và D.
Xét hai ∆MAC và ∆MBD:
ˆAMC=ˆBMDAMC^=BMD^ (đối đỉnh)
ˆA=ˆDA^=D^ (hai góc nội tiếp cùng chắn cung BCBC⏜
Suy ra: ∆MAC đồng dạng ∆MDB (g.g)
⇒MBMC=MDMA⇒MBMC=MDMA
⇒MA.MB=MC.MD⇒MA.MB=MC.MD (1)
Vì M, O cố định suy ra điểm C và D cố định nên độ dài của các đoạn MC và MD không đổi ⇒⇒ tích MC.MD không đổi (2)
Từ (1) và (2) suy ra tích MA. MB không đổi khi cát tuyến AB thay đổi.
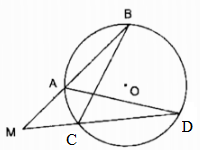
Trường hợp điểm M ở ngoài đường tròn (O)
Kẻ cát tuyến MAB bất kỳ của (O) và đường thẳng MO cắt đường tròn (O) tại C và D
Xét ∆MAD và ∆MCB:
ˆMM^ chung
ˆB=ˆDB^=D^ (hai góc nội tiếp cùng chắn cung ACAC⏜)
Suy ra: ∆MAD đồng dạng ∆MCB (g.g)
⇒MC.MA=MB.MD⇒MA.MB=MC.MD⇒MC.MA=MB.MD⇒MA.MB=MC.MD (3)
Vì M và O cố định suy ra điểm C, D cố định nên độ dài của các đoạn MC và MD không đổi ⇒⇒ tích MC. MD không đổi (4)
Từ (3) và (4) suy ra tích MA. MB không đổi khi cát tuyến MAB thay đổi.
Từ một điểm M cố định ở bên ngoài đường tròn (O), kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. Chứng minh rằng luôn có M T 2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB
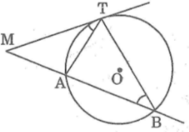

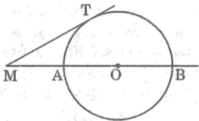
Vì cát tuyến MAB kẻ tùy ý nên ta luôn có M T 2 = MA.MB không phụ thuộc vị trí của cát tuyến MAB.
25. Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. a) Chứng minh ta luôn có MT2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB b) Ở hình 2 cho MT = 20, MB=50cm, tính bán kính đường tròn
mình không biết đâu chỉ có thánh mới giải được
Xét \(\Delta\)MTA và \(\Delta\)MBT
có: góc M chung
\(\widehat{MTA}=\widehat{MBT}\left(=\frac{1}{2}\widebat{AT}\right)\)
=> \(\Delta\)MTA đồng dạng \(\Delta\)MBT
=> \(\frac{MT}{MB}=\frac{MA}{MT}\Rightarrow MT^2=MA.MB\left(ĐPCM\right)\)
do MT là tiếp tuyến mà M cố định nên => MT không đổi, do vậy MA.MB không đổi
Cho đường tròn (O;R) cố định và đường thằng d không đi qua O cắt (O;R) tại a và b. Từ điểm M bất kì trên d và ở ngoài đường tròn vẽ hai tiếp tuyến MN;MP (N và P là hai tiếp điểm)
1) Chứng minh MNOP nội tiếp.Gọi O' là tâm đường tròn này, xác định vị trí
2) Đường tròn (O') ngoại tiếp tứ giác MNOP cắt d tại I.Chứng minh IA=IB
3) Từ N kẻ đường kính ND của (O) và đường kính NC của (O'). Cm tích DP.DC không đổi
4) Xác định vtrí của M trên d sao cho MNOP là hình vuông.
Giúp mình câu 3 và 4 với nhé!
1) Xét tứ giác MNOP có
\(\widehat{ONM}\) và \(\widehat{OPM}\) là hai góc đối
\(\widehat{ONM}+\widehat{OPM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MNOP là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Tâm của đường tròn ngoại tiếp tứ giác MNOP là trung điểm của OM
hay O' là trung điểm của OM
25. Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
a) Chứng minh ta luôn có MT2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB
b) Ở hình 2 cho MT = 20, MB=50cm, tính bán kính đường tròn
Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E.
c) Chứng minh rằng OM.OD + ON.OE không đổi
c) Xét tam giác DOC vuông tại C, CM là đường cao có:
OM.OD = OC 2 = R 2
Xét tam giác EOC vuông tại C, CN là đường cao có:
ON.OE = OC 2 = R 2
Khi đó: OM.OD + ON.OE = 2 R 2
Vậy OM.OD + ON.OE không đổi
Cho đường tròn (O) và đường thẳng xy không có điểm chung với đường tron f(O). Gọi A là hình chiếu của O trên đường thẳng xy. Qua A vẽ cát tuyến không đi qua O cắt đường tròn tại hai điểm B và C (AB < AC). Tiếp tuyến của đường tròn tại hai điểm B và C cắt đường thẳng xy lần lượt taiij M và N.
a) Chứng minh tứ giác ABOM nội tiếp.
b) Chứng minh góc BCO bằng góc ANO và tam giác OMN cân.
c) Giả sử đường tròn (O) và đường thẳng xy cố định. Từ M vẽ tiếp tuyến thứ hai ME với đường tròn (O), E là tiếp điểm khác B. Chứng minh khi cát tuyến ABC di chuyển quanh A thì BE luôn đi qua một điểm cố định.
GIÚP MÌNH CÂU C VỚI!!!
Vẽ hình bài này bằng ứng dụng của web khó quá. Mình loay hoay k được. Bạn chịu khó vẽ hình giải giúp mình bạn nhé!
Cho đường tròn (O) đường kính AB. Gọi C là điểm cố định trên OA. M là điểm di động trên đường tròn. Qua M kẻ đường vuông góc với MC cắt các tiếp tuyến kẻ từ A và B ở D và E. a. Chứng minh rằng tam giác DCE vuông. b. Chứng minh rằng tích AD.BE không đổi khi M di động. c. Chứng minh rằng khi M chạy thì trung điểm I của DE chạy trên một đường thẳng cố định