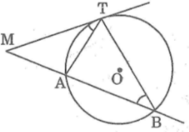
Vì cát tuyến MAB kẻ tùy ý nên ta luôn có M T 2 = MA.MB không phụ thuộc vị trí của cát tuyến MAB.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
25. Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. a) Chứng minh ta luôn có MT2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB b) Ở hình 2 cho MT = 20, MB=50cm, tính bán kính đường tròn
25. Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
a) Chứng minh ta luôn có MT2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB
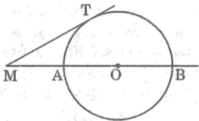
b) Ở hình 2 cho MT = 20, MB=50cm, tính bán kính đường tròn
4. Từ M cố định bên ngoài đường tròn (o) kẻ môt tiếp tuyến MT ( T là tiếp điểm ) và một cát tuyến MAB của đường tròn đó
a) Chứng minh MT2 = MA.MB
b) trường hợp cát tuyến MAB đi qua tâm (o) . Cho MT = 20 (cm) và cát tuyến dài nhất cũng xuất phát từ M = 50 (cm) . Tính R của (O)
Giúp em bài này với mai em cần gấp !
Từ một điểm M cố định ở bên ngoài đường tròn (O), kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. Cho MT = 20cm ,MB = 50cm,tính bán kính đường tròn
Từ một điểm M bên ngoài đường tròn (O) kẻ tiếp tuyến MT và cát tuyến MAb. Vẽ đường tròn (O') ngoại tiếp tam giác MAT. Từ M vẽ tiếp tuyến xy của đường tròn (O').Chứng minh rằng:
a, MT2=MA.MB
b, BT//xy
Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cát tuyến MAB.
Chứng minh M T 2 = M A . M B .
từ 1 điểm M cố định ở bên ngoài đường tròn (O), kẻ 1 tiếp tuyến MT(T là tiếp điểm) và 1 cát tuyến MAB của đường tròn đó
a)C/m: MT2=MA.MB
b) trường hợp cát tuyến MAB đi qua tâm O. cho MT=20cm và cát tuyến dài nhất cùng xuất phát từM=50cm. tính bán kính R của đường tròn tâm O
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn đó. qua điểm M kẻ tiếp tuyến MT và cát tuyến MAB với đường tròn. chứng minh MT2 =MA.MB
Cho đườn tròn (O) và điểm M nằm bên ngoài đường tròn. Qua điểm M kẻ tiếp tuyến MT và đường tròn ( T là tiếp điểm) và cát tuyến MAB (A nằm giữa M và B).
a) So sánh hai góc ATM và góc ABT ;
b) Chứng minh MT2 = MA.MB.