Với \(m\) bất kì, chứng tỏ :
a) \(1+m< 2+m\)
b) \(m-2< 3+m\)
Những câu hỏi liên quan
Với m bất kì, hãy chứng tỏ: m – 2 < 3 + m
Với m bất kì, hãy chứng tỏ: 1 + m < 2 + m
Với số m và số n bất kì, chứng tỏ rằng :
a) \(\left(m+1\right)^2\ge4m\)
b) \(m^2+n^2+2\ge2\left(m+n\right)\)
a. Ta có:
\(\left(m+1\right)^2\)\(=m^2+2m+1\)
\(\left(m+1\right)^2\ge4m\Leftrightarrow m^2+2m+1\ge4m\)
\(\Leftrightarrow m^2+2m+1-4m\ge0\)
\(\Leftrightarrow m^2-2m+1\ge0\)
\(\Leftrightarrow\left(m-1\right)^2\ge0\) (đúng \(\forall\) m)
Vậy \(\left(m+1\right)^2\ge4m\)
b. \(m^2+n^2+2\ge2\left(m+n\right)\)
\(\Leftrightarrow m^2+1+n^2+1\ge2m+2n\)
Ta có:
\(\left(m^2+1\right)^2\ge4m^2\) \(\Rightarrow m^2+1\ge2m\)
\(\left(n^2+1\right)^2\ge4n^2\Rightarrow n^2+1\ge2n\)
Đúng 0
Bình luận (0)
Với số m và số n bất kì,chứng tỏ rằng:
a) \(\left(m+1\right)^2\ge4m\)
b)\(m^2+n^2+2\ge2\left(m+n\right)\)
a ) \(\left(m+1\right)^2\ge4m\)
\(\Leftrightarrow m^2+2m+1\ge4m\)
\(\Leftrightarrow\left(m^2+2m+1\right)-4m\ge0\)
\(\Leftrightarrow m^2-2m+1\ge0\)
\(\Rightarrow\left(m-1\right)^2\ge0\) (luôn đúng) (ĐPCM)
b ) \(m^2+n^2+2\ge2\left(m+n\right)\)
\(\Leftrightarrow m^2+n^2+2-2m-2n\ge0\)
\(\Leftrightarrow\left(m^2-2m+1\right)+\left(n^2-2n+1\right)\ge0\)
\(\Leftrightarrow\left(m-1\right)^2+\left(n-1\right)^2\ge0\)(luôn đúng) |(ĐPCM)
Đúng 0
Bình luận (0)
Với số m và số n bất kì, chứng tỏ rằng: m 2 + n 2 + 2 ≥ 2(m + n)
Ta có: m - 1 2 ≥ 0; n - 1 2 ≥ 0
⇒ m - 1 2 + n - 1 2 ≥ 0
⇔ m 2 – 2m + 1 + n 2 – 2n + 1 ≥ 0
⇔ m 2 + n 2 + 2 ≥ 2(m + n)
Đúng 0
Bình luận (0)
Với số m và số n bất kì, chứng tỏ rằng: m + 1 2 ≥ 4m
Ta có: m + 1 2 ≥ 0
⇔ m - 1 2 + 4m ≥ 4m
⇔ m 2 – 2m + 1 + 4m ≥ 4m
⇔ m 2 + 2m + 1 ≥ 4m
⇔ m + 1 2 ≥ 4m
Đúng 0
Bình luận (0)
chứng tỏ rằng với bất kỳ giá trị nào của m thì các bất đẳng thức sau luôn
luôn đúng
a. 10 m 2 – 5m +1 $\geq$ m 2 + m
b. m 2 - m $\leq$ 50m 2 – 15m + 1
Chứng tỏ rằng với 2 số tự nhiên bất kì khi chia cho m có cùng số dư thì hiệu của chúng chia hết cho m và ngược lại
Cho 2 tia Oa và Ob không đối nhau .Trên tia Oa lấy điểm A không trùng với điểm O,trên tia Ob lấy điểm B không trùng với điểm O . Gọi C là 1 điểm bất kì nằm giữa A và B . Vẽ điểm M sao cho O nằm giữa C và M Chứng tỏ tia OC nằm giữa 2 tia OA và OB Trong 3 tia tia nào nằm giữa 2 tia còn lại?
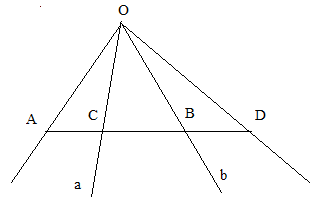
Vì C nằm giữa A và B nên tia OC nằm giữa hai tia OA, OB
Vì D không nằm giữa A và B nên tia OD không nằm giữa hai tia OA và OB.