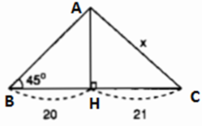
Tìm x trong hình 23 ?

Tìm x trong hình 23.
Hình 23
Kí hiệu như hình trên.
Ta có tam giác ABH là vuông cân (vì ∠B = 45o) nên AH = 20.
Áp dụng định lí Pitago trong tam giác vuông AHC có:
x2 = AH2 + HC2 = 202 + 212 = 841
=> x = √841 = 29
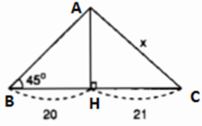
Tìm x trong hình 23.
Hình 23
Kí hiệu như hình trên.
Ta có tam giác ABH là vuông cân (vì ∠B = 45o) nên AH = 20.
Áp dụng định lí Pitago trong tam giác vuông AHC có:
x2 = AH2 + HC2 = 202 + 212 = 841
=> x = √841 = 29
Tính các độ dài \(x,y\) trong Hình 23.
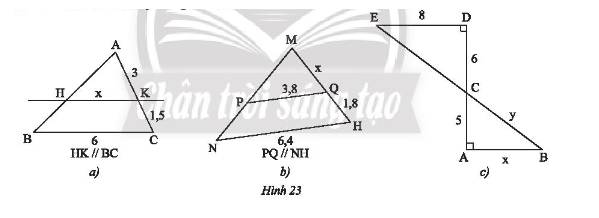
a) Ta có: \(AC = AK + KC = 3 + 1,5 = 4,5\)
Xét tam giác \(ABC\) có \(HK//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{HK}}{{BC}} = \frac{{AK}}{{AC}} \Rightarrow \frac{x}{6} = \frac{3}{{4,5}}\). Do đó, \(x = \frac{{3.6}}{{4,5}} = 4\).
Vậy \(x = 4\).
b) Ta có: \(MH = MQ + QH = x + 1,8\)
Xét tam giác \(MNH\) có \(PQ//NH\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{PQ}}{{NH}} = \frac{{MQ}}{{MH}} \Rightarrow \frac{{3,8}}{{6,4}} = \frac{x}{{x + 1,8}}\). Do đó, \(6,4x = 3,8.\left( {x + 1,8} \right)\)
\( \Leftrightarrow 6,4x = 3,8x + 6,84\)
\( \Leftrightarrow 6,4x - 3,8x = 6,84\)
\( \Leftrightarrow 2,6x = 6,84\)
\( \Leftrightarrow x = 6,84:2,6\)
\( \Leftrightarrow x = \frac{{171}}{{65}}\).
Vậy \(x = \frac{{171}}{{65}}\).
c) Vì \(\left\{ \begin{array}{l}DE \bot AD\\AB \bot AD\end{array} \right. \Rightarrow DE//AB\) (quan hệ từ vuông góc đến song song).
Xét \(\Delta CDE\) vuông tại \(D\) ta có:
\(E{D^2} + D{C^2} = E{C^2}\) (Định lí Py- ta – go)
\( \Leftrightarrow {8^2} + {6^2} = E{C^2}\)
\( \Leftrightarrow E{C^2} = 100\)
\( \Leftrightarrow EC = 10\)
Xét tam giác \(ABC\) có \(DE//AB\) nên theo hệ quả của định lí Thales ta có:
\(\left\{ \begin{array}{l}\frac{{AC}}{{DC}} = \frac{{AB}}{{ED}} \Rightarrow \frac{5}{6} = \frac{x}{8}\\\frac{{AC}}{{DC}} = \frac{{BC}}{{EC}} \Rightarrow \frac{5}{6} = \frac{y}{{10}}\end{array} \right.\). Do đó, \(\left\{ \begin{array}{l}x = \frac{{5.8}}{6} = \frac{{20}}{3}\\y = \frac{{5.10}}{6} = \frac{{25}}{3}\end{array} \right.\).
Vậy \(x = \frac{{20}}{3};y = \frac{{25}}{3}\).
Phân tử X2Y có tổng số proton là 23. Biết X, Y ở hai nhóm A liên tiếp trong cùng một chu kì. Dựa vào cấu hình electron các nguyên tử X, Y. Tìm công thức phân tử và gọi tên hợp chất X2Y
A. NO2
B. CO2
C. H2S
D. H2O
Đáp án A
Đặt số proton của X, Y là ZX, ZY
Ta có 2ZX + ZY = 23 (1)
- Nếu X trước Y thì ZY = ZX + 1 (2)
Từ (1) và (2) → 2ZX + ZX + 1 = 23→ ZX = 22/3 = 7,3 (vô lí)
- Nếu Y trước X thì ZX = ZY + 1 (3)
Từ (1) và (3) → 2( ZY + 1) + ZY = 23 → 3ZY = 21
ZY = 7 → Y là nito (N)
ZX = 8 → X là oxi (O)
Công thức X2Y là NO2
Tìm sai lầm trong các "lời giải" sau:
a) Giải bất phương trình -2x > 23. Ta có:
-2x > 23 ⇔ x > 23 + 2 ⇔ x > 25.
Vậy nghiệm của bất phương trình là x > 25.
b) Giải bất phương trình 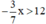 . Ta có:
. Ta có:
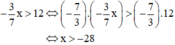
a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.
Lời giải đúng:
-2x > 23
⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)
⇔ x < -11,5
Vậy nghiệm của bất phương trình là x < -11,5
b) Sai lầm là nhân hai vế của bất phương trình với 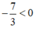 mà không đổi chiều bất phương trình.
mà không đổi chiều bất phương trình.
Lời giải đúng:
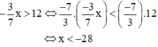
Vậy nghiệm của bất phương trình là x < -28
Tìm x trong các tỉ lệ thức sau:
1 3 . x : 2 3 = 1 3 4 : 2 5
Tìm x trong mỗi hình vẽ sau biết CI và BI là 2 p/g của góc ACB và góc ABC, còn EH và FH là 2 p/g của góc DEF và góc DFE
GIÚP MÌNH VỚI
Tìm x trong các tỉ lệ thức sau: 1 1 3 : 0 , 8 = 2 3 : ( 0 , 1 x )
Tìm x trong các tỉ lệ thức sau: 1 5 x : 3 = 2 3 : 0 , 25