Tính thể tích của mỗi hình chóp đều dưới đây (h.130 và h.131)
Những câu hỏi liên quan
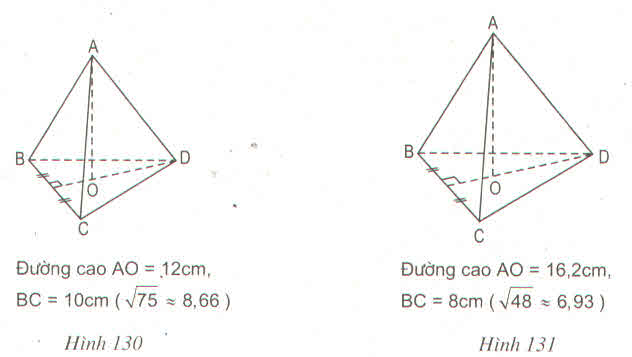
Tính thể tích của mỗi hình chóp đều dưới đây (h.130, h.131).
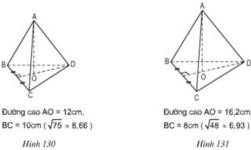
Tính thể tích của hình chóp đều, hình chóp cụt đều sau đây (h.147 và h.148) (√3 ≈ 1,73)
Hướng dẫn: Hình chóp L.EFGH cũng là hình chóp đều.
Sách giáo khoa Toán 8 tập 1 Chân trời sáng tạo
21 tháng 7 2023 lúc 20:59
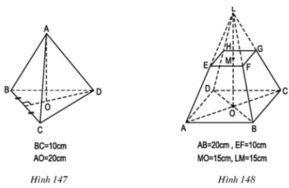
a) Tính diện tích xung quanh của mỗi hình chóp tứ giác đều dưới đây.
b) Cho biết chiều cao của hình chóp tứ giác đều trong Hình 9a và Hình 9b lần lượt là 4cm và \(12\)cm. Tính thể tích của mỗi hình.
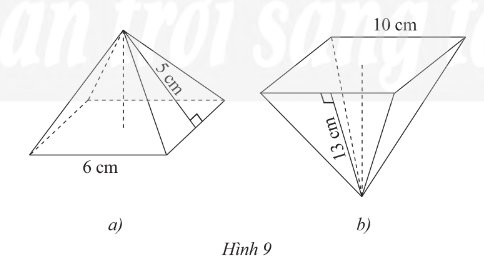
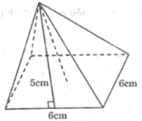
Tính thể tích và diện tích toàn phần của hình chóp đều dưới đây theo kích thước cho trên hình
Đường cao hình chóp bằng: 13 2 - 5 2 = 144 = 12 cm
Diện tích đáy bằng:S = 10.10 = 100 ( c m 2 )
Thể tích hình chóp bằng : V=1/3 S.h=1/3 .100.12=400 ( c m 3 )
Diện tích xung quanh bằng: S x q = Pd = 10.2.13 = 260 ( c m 2 )
Diện tích toàn phần là : S T P = S x q + S đ á y = 260 + 100 = 360 ( c m 2 )
Đúng 0
Bình luận (0)
Tính thể tích và diện tích toàn phần của hình chóp đều dưới đây theo kích thước cho trên hình
Đường cao hình chóp bằng: 5 2 - 3 2 = 25 - 9 = 16 = 4 cm
Diện tích đáy bằng:S = 6.6 = 36 ( c m 2 )
Thể tích hình chóp bằng : V=1/3 S.h=1/3 .36.4=48 ( c m 3 )
Diện tích xung quanh bằng: S x q = Pd=2.6.5=60 ( c m 2 )
Diện tích toàn phần là : S T P = S x q + S đ á y = 60 + 36 = 96 ( c m 2 )
Đúng 0
Bình luận (0)
Tính thể tích của hình chóp đều, hình chóp cụt đều dau đây (h.147, h.148) (\(\sqrt{3}\approx1,73\))
Hướng dẫn : Hình chóp L.EFGH cũng là hình chóp đều
Cho hình chóp đều S.ABC, có tất cả các cạnh bằng nhau và đều bằng 4 cm.a) Xác định vị trí chân đường cao H của hình chóp S.ABC và tính độ dài đoạn SH.b) Tính diện tích xung quanh hình chóp.c) Tính diện tích toàn phần của hình chóp.d) Tính thể tích hình chóp.
Đọc tiếp
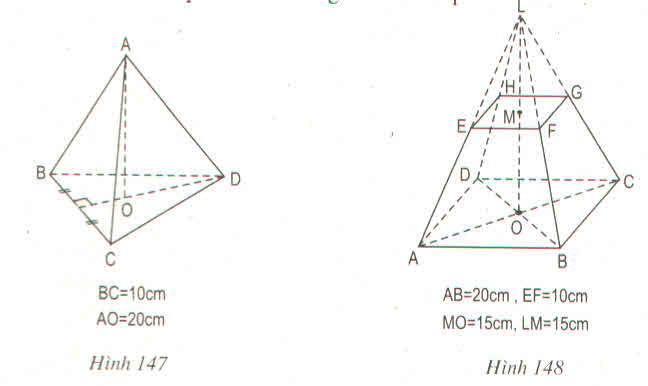
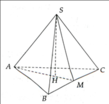
Cho hình chóp đều S.ABC, có tất cả các cạnh bằng nhau và đều bằng 4 cm.
a) Xác định vị trí chân đường cao H của hình chóp S.ABC và tính độ dài đoạn SH.
b) Tính diện tích xung quanh hình chóp.
c) Tính diện tích toàn phần của hình chóp.
d) Tính thể tích hình chóp.
a) Chân đường cao H của hình chóp S.ABC trùng với trọng tâm của tam giác ABC.
Gọi M là trung điểm của BC
Tam giác ABC có
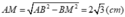
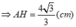
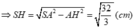
b) Tam giác SAM cân ở M nên
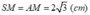
Diện tích xung quanh của hình chóp:
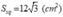
c) Diện tích toàn phần của hình chóp:
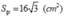
d) Thể tích của hình chóp
Đúng 0
Bình luận (0)
Cho hình chóp tam giác đều có cạnh bên là b và chiều cao là h (b h). Tính thể tích của khối chóp đó. A.
V
3
4
b
2
-
h
2
h
B.
V
3
12
b
2...
Đọc tiếp
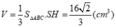
Cho hình chóp tam giác đều có cạnh bên là b và chiều cao là h (b > h). Tính thể tích của khối chóp đó.
A. V = 3 4 b 2 - h 2 h
B. V = 3 12 b 2 - h 2 h
C. V = 3 8 b 2 - h 2 h
D. V = 3 4 b 2 - h 2 b
Đáp án A
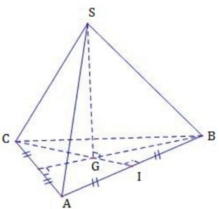
Phương pháp:
+) Gọi G là trọng tâm tam giác ABC ⇒ SG ⊥(ABC)
+) Tính diện tích tam giác đều ABC theo b và h.
+) Sử dụng công thức tính thể tích khối chóp 
Cách giải:
Gọi G là trọng tâm tam giác ABC ⇒ SG ⊥(ABC)
Tam giác SCG vuông tại G
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng
a
3
. Tính chiều cao h của hình chóp đã cho. A. h
3
a B. h
a
3
2
C. h
a
3
3
D. h
a
3
6
Đọc tiếp
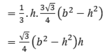
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng a 3 . Tính chiều cao h của hình chóp đã cho.
A. h = 3 a
B. h = a 3 2
C. h = a 3 3
D. h = a 3 6
Xét hình chóp S.ABC có đáy ABC là tam giác đều cạnh 
Thể tích khối chóp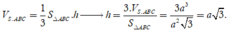 
Chọn A.
Đúng 0
Bình luận (0)