Cho f(x)=ax3+bx2+cx+d (x # 0) có nghiệm là 1 và -1
a) Tìm mối quan hệ giữa a,b,c,d
b) Tìm nghiệm còn lại của f(x)
Cho đa thức: f(x)=x4+ax3+bx2+cx+df(x)=x4+ax3+bx2+cx+d ( với a, b, c, d là các số thực). Biết f(1)=10; f(2)=20; f(3)=30. Tính giá trị của biểu thức: A=f(9)+f(-5
)
Đặt \(g\left(x\right)=f\left(x\right)-10\) (bậc 4)
\(\Leftrightarrow\left\{{}\begin{matrix}g\left(1\right)=0\\g\left(2\right)=0\\g\left(3\right)=0\end{matrix}\right.\Leftrightarrow g\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)\) (m là hằng số)
\(\Leftrightarrow f\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)-10\\ \Leftrightarrow f\left(9\right)=8\cdot7\cdot6\left(9-m\right)-10=336\left(9-m\right)-10\\ f\left(-5\right)=\left(-6\right)\left(-7\right)\left(-8\right)\left(-5-m\right)-10=336\left(m+5\right)-10\)
Vậy \(A=336\left(9-m\right)+336\left(m+5\right)-20=4684\)
Chúc bạn hok tốt <3
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d , ( a ≠ 0 ) . Khẳng định nào sau đây đúng
A. l i m x → - ∞ x = + ∞
B. Đồ thị hàm số luôn cắt trục hoành
C. Hàm số luôn tăng trên R
D. Hàm số luôn có cực trị
Cho hàm số bậc 3 có dạng: y = f ( x ) = a x 3 + b x 2 + c x + d .
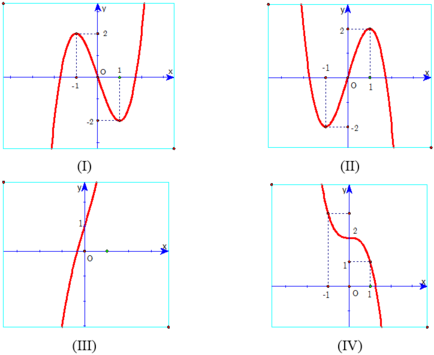
Hãy chọn đáp án đúng?
A. Đồ thị IV xảy ra khi a > 0 và f ' ( x ) = 0 có nghiệm kép.
B. Đồ thị I I xảy ra khi a ≠ 0 và f ' ( x ) = 0 có hai nghiệm phân biệt.
C. Đồ thị I xảy ra khi a < 0 và f ' ( x ) = 0 có hai nghiệm phân biệt.
D. Đồ thị III xảy ra khi a > 0 và f ' ( x ) = 0 vô nghiệm.
Chọn D .
Hàm số của đồ thị (II) có a < 0 nên điều kiện a ≠ 0 chưa đảm bảo. Do đó loại phương án B.
Hàm số của đồ thị (I) có a > 0 nên loại luôn phương án C.
Hàm số của đồ thị (IV) có a < 0 nên loại luôn phương án D.
Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d ( a ≠ 0 ) có đồ thị như hình vẽ. Phương trình f (f(x)) có bao nhiêu nghiệm thực?

A. 5.
B. 3.
C. 7.
D. 9.
Đáp án D
Đặt ![]() , phương trình
, phương trình ![]() trở thành
trở thành ![]() .
.
Nhìn vào đồ thị ta thấy phương trình ![]() có 3 nghiệm
có 3 nghiệm ![]() thuộc khoảng
thuộc khoảng ![]() , với mỗi giá trị t như vậy phương trình
, với mỗi giá trị t như vậy phương trình ![]() có 3 nghiệm phân biệt.
có 3 nghiệm phân biệt.
Vậy phương trình ![]() có 9 nghiệm.
có 9 nghiệm.
Cho hàm số f ( x ) = ax 3 + bx 2 + cx + d có đồ thị như hình vẽ dưới đây. Số nghiệm của phương trình f(x)+1= 0 là
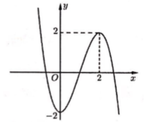
A. 0
B. 3
C. 2.
D. 1
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( a ≠ 0 ) có đồ thị như hình vẽ:
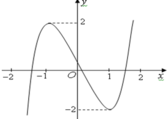
Phương trình f(f(x))=0 có bao nhiêu nghiệm thực?
A. 3
B. 7
C. 9
D. 5
b) Cho f(x)=ax3+bx2+cx+d , trong đó a,b,c,d là hằng số và thoả mãn: b=3a+c, Chứng tỏ rằng: f(1)=f(2)
Thay b = 3a + c vào f(x) ta được:
f(x) = ax3 + (3a+c)x2 + cx + d
⇒ f(1) = a.13 + 3a + c.12+ c.1 + d
= a + 3a + c + c + d
= 4a + 2c + d
= 4a + 2c + d (1)
f(2) = a.23 + 3a + c.22 - c.2 + d
= 8a + 3a + 4c - 2c + d
= 4a + 2c + d (2)
Từ (1) và (2) ➩ f(1) = f(2) [= 4a + 2 + d]
Cho hàm số y = f x = a x 3 + b x 2 + c x + d Biết f x + 1 = x 3 + 3 x 2 + 3 x + 2 hãy xác định biểu thức f(x)
A. f x = x 3 + 1
B. f x = x 3 + 3 x + 2
C. f x = x 3 + 3 x 2
D. f x = x 3 + 3 x 2 + 3 x + 1
Đáp án A
Ta có f x + 1 = x 3 + 3 x 2 + 3 x + 2 = x + 1 3 + 1 ⇒ f x = x 3 + 1
Cho hàm số f ( x ) = ax 3 + bx 2 + cx + d có đồ thị như hình vẽ bên dưới
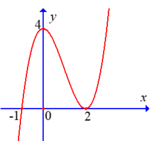
Mệnh đề nào sau đây sai?
A. Hàm số đạt cực tiểu tại x=2.
B. Hàm số đạt cực đại tại x=4.
C. Hàm số có hai điểm cực trị.
D. Hàm số đạt cực đại tại x=0.
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d ( a ≠ 0 ) có đồ thị như hình vẽ. Số nghiệm của phương trình 3f(x) -1 =0 bằng

A. 0
B. 1
C. 2
D. 3