Trong các giá trị \(t=-1;t=0;t=1\), giá trị nào là nghiệm của phương trình :
\(\left(t+2\right)^2=3t+4\)
Trong các giá trị t = -1, t = 0 và t = 1, giá trị nào là nghiệm của phương trình: (t + 2)2 = 3t + 4?
Lần lượt thay các giá trị của t vào hai vế của phương trình ta được:
- Tại t = -1 :
(t + 2)2 = (-1 + 2)2 = 1
3t + 4 = 3(-1) + 4 = 1
⇒ t = -1 là nghiệm của phương trình (t + 2)2 = 3t + 4.
- Tại t = 0
(t + 2)2 = (0 + 2)2 = 4
3t + 4 = 3.0 + 4 = 4
⇒ t = 0 là nghiệm của phương trình (t + 2)2 = 3t + 4.
- Tại t = 1
(t + 2)2 = (1 + 2)2 = 9
3t + 4 = 3.1 + 4 = 7
⇒ t = 1 không là nghiệm của phương trình (t + 2)2 = 3t + 4.
Bài 1.
a) Kiểm tra xem trong giá trị y = -2, y = 1, giá trị nào là nghiệm của phương trình (y + 1)2 = 2y + 5.
b) Kiểm tra xem trong các giá trị x = -3, x = 1, giá trị nào là nghiệm của phương trình (x + 2)2 = 4x + 5.
c) Kiểm tra xem trong các giá trị t = -1, t = 3, giá trị nào là nghiệm của phương trình (2t + 1)2 = 4t + 5.
d) Kiểm tra xem trong các giá trị z = -2, z = 1, giá trị nào là nghiệm của phương trình (z + 3)2 = 6z + 10.
a, +) Thay y = -2 vào phương trình trên ta có :
( -2 + 1 )2 = 2 . ( -2 ) + 5
1 = 1
Vậy y = -2 thỏa mãn phương trình trên
+) Thay y = 1 vào phương trình trên , ta có :
( 1 + 1)2 = 2 . 1 + 5
4 = 7
Vậy y = 1 thỏa mãn phương trình trên
b, +) Thay x =-3 vaò phương trình trên , ta có :
( -3 + 2 )2 = 4 . ( -3 ) + 5
2 = -7
Vậy x = -3 không thỏa mãn phuong trình trên
+) Thay x = 1 vào phương trình trên , ta có :
( 1 + 2 )2 = 4 . 1 + 5
9 = 9
Vậy x = 1 thỏa mãn phương trình trên
c, +) Thay t = -1 vào phương trình , ta có :
[ 2 . ( -1 ) + 1 ]2 = 4 . ( -1 ) + 5
1 = 1
Vậy t = -1 thỏa mãn phương trình trên
+) Thay t = 3 vào phương trình trên , ta có :
( 2 . 3 + 1 )2 = 4 . 3 + 5
49 = 17
Vậy t = 3 không thỏa mãn phương trình trên
d, +) Thay z = -2 vào phương trình trên , ta có :
( -2 + 3 )2 = 6 . ( -2 ) + 10
1 = -2
Vậy z = -2 không thỏa mãn phương trình trên
+) Thay z = 1 vào phương trình trên , ta có :
( 1 + 3 )2 = 6 . 1 + 10
16 = 16
Vậy z =1 thỏa mãn phương trình trên
tìm giá trị lớn nhất của A= Ix-yI+Iz-tI trong đó x,y,z,t là các số nguyên khác nhau nhận các giá trị từ 1 đến 2003
giúp mình nha
tìm giá trị lớn nhất của A= Ix-yI+Iz-tI trong đó x,y,z,t là các số nguyên khác nhau nhận các giá trị từ 1 đến 2003
giúp mình nha! Mình vội lắm
Các giá trị tương ứng của t và s được cho trong bảng sau:
| t | 1 | 2 | 3 | 4 | 5 |
| s | 12 | 24 | 36 | 48 | 60 |
| s/t |
các số Điền thích hợp vào các ô trống trong bảng trên
Điền số thích hợp vào ô trống:
| t | 1 | 2 | 3 | 4 | 5 |
| s | 12 | 24 | 36 | 48 | 60 |
| s/t | 12 | 12 | 12 | 12 | 12 |
Tìm gtln của A=|x-y|+|z-t|,trong đó x,y,z,t là các số nguyên khác nhau nhận các giá trị từ 1 đến 2003
Giả sử x > y, z > t.
Ta có \(A=x-y+z-t\le\left(2023+2022\right)-\left(1+2\right)=4042\).
Dấu bằng xảy ra khi x = 2023; y=1; z = 2022; t = 1.
1. Phân tích chi tiết nghệ thuật 'cái bóng' trong truyện Người con gái Nam Xương.
2. Phân tích giá trị các yếu tố kì ảo trong truyện Người con gái Nam Xương
3. Tóm tắt truyện Người con gái Nam Xương
4. Nêu các giá trị nội dung + nghệ thuật của truyện Người con gái Nam Xương
5. Nêu nghệ thuật xây dựng nhân vật của Nguyễn Du qua 2 đoạn trích 'Chị em Thúy Kiều' và 'Kiều ở lầu Ngưng Bích'
Trong các cặp số (x,y) thỏa mãn log x 2 + y 2 x + y ≥ 1 , hãy tìm giá trị lớn nhất của T = x + 2 y .
A. 3 + 5 2
B. 3 + 2 5 2
C. 3 + 10 2
D. 2 + 10 2
Cho phương trình: 4 cos 2 x + 16 sin x cos x - 7 = 0 ( 1 )
Xét các giá trị:
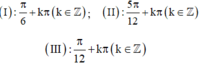
Trong các giá trị trên, giá trị nào là nghiệm của phương trình (1)?
A. Chỉ (III)
B. (II) và (III)
C. Chỉ (II)
D. Chỉ (I)
Đ á p á n B P T đ ã c h o t ư ơ n g đ ư ơ n g : 4 . cos 2 2 x + 8 sin 2 x - 7 = 0 ⇔ 4 . 1 - sin 2 2 x + 8 . sin 2 x - 7 = 0 ⇔ - 4 . sin 2 2 x + 8 . sin 2 x - 3 = 0 ⇔ sin 2 x = 1 2 ⇔ x = π 12 + k π ( k ∈ ℤ ) hoặc x = 5 π 12 + kπ ( k ∈ ℤ )