Cho hình 82, trong đó MD // Ab và ME // AC. Chứng minh rằng điểm A đối xứng với M qua I
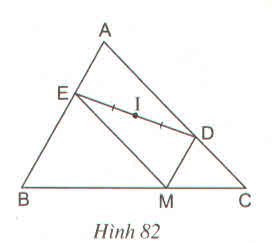
Cho hình 82, trong đó MD // AB và ME // AC. Chứng minh rằng điểm A đối xứng với điểm M qua điểm I.
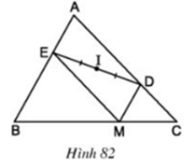
Ta có: MD// AE (vì MD// AB)
ME // AD (vì ME // AC)
Nên AEMD là hình bình hành, I là trung điểm của DE nên I cũng là trung điểm của AM, do đó A đối xứng với M qua I.
cho tam giác ABC, e thuộc AB,d thuộc AC, M thuộc BC, I là trung điểm của ED.Trong đó MD // AB và ME // AC. Chứng minh rằng điểm A đối xứng với điểm M qua điểm I.
Ta có: EM//AC => EM//AD
MD//AB => MD//AE
=> AEMD là hình bình hành
I là trung điểm của ED => I là trung điểm của AM => I thuộc AM
=> AIM=180
Cho Tam giác ABC . trên cạnh AB,AC,BC lần lượt lấy các điểm E,D,M sao cho MD//AB và ME//AC gọi I là trung điểm ED
a) Tứ giác AEMD là hình gì
B) Chứng minh rằng điểm A đối xứng với điểm M qua điểm I
a: Xét tứ giác AEMD có
AE//MD
AD//ME
Do đó: AEMD là hình bình hành
Cho tam giác ABC vuông tại A và M là trung điểm cạnh BC. kẻ MD vuông góc với AB (D thuộc AB) và ME vuông góc với AC (E thuộc AC)
a)chứng minh tứ giác ADME là hình chữ nhật
b)gọi P là điểm đối xứng của M qua D; Q là điểm đối xứng của M qua E . Chứng minh tứ giác PAMB là hình thoi
c)P đối xứng với Q qua A
a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
nên ADME là hình chữ nhật
b: Xét tứ giác AMBP có
D là trung điểm chung của AB và MP
MA=MB
Do đó: AMBP là hình thoi
=>ABlà phân giác của góc MAP(1)
c: Xét tứ giác AMCQ có
E là trung điểm chung của AC và MQ
MA=MC
Do đó: AMCQ là hình thoi
=>AC là phân giác của góc MAQ(2)
Từ (1), (2) suy ra góc PAQ=2*90=180 độ
=>P,A,Q thẳng hàng
mà AP=AQ
nên A là trung điểm của PQ
Cho tam giác ABC và điểm M nằm bên trong tam giác đó. Vẽ MD song song với AB (D thuộc AC), ME song song với AC (E thuộc AB). Vẽ điểm F đối xứng với M qua đường thẳng DE. Chứng minh : Tứ giác AFDE là hình thang cân.
Cho tam giác ABC vuông tại A,M là trung điểm của BC . Từ M kẻ MD vuông góc với AB và ME vuông góc với AC
a) Chứng minh : tứ giác adme là hình chữ nhật
b) Gọi P là điểm đối xứng của D qua M , Q là điểm đối xứng của E qua M . Chứng minh DEPQ là hình thoi
c) Chứng minh : BC=2DQ
d) BQ cắt CP tại I . Chứng minh ba điểm A,M,I thẳng hàng
Cho ΔABC vuông tại A từ trung điểm M của cạnh BC, kẻ MD và ME lần lượt vuông góc với AB và AC ( E ∈ AB, D ∈ AC). Lấy điểm F đối xứng với M qua Ea) Chứng minh tứ giác AMCF là hình thoib) Tìm điều kiện để ΔABC để tứ giác AMCE là hình vuôngc) Gọi I là trung điểm của EM. Chứng minh I là trung điểm của CD
a) Xét ΔAMF có
AE là đường cao ứng với cạnh MF(\(AE\perp MF\))
AE là đường trung tuyến ứng với cạnh MF(E là trung điểm của MF)
Do đó: ΔAMF cân tại A(Định lí tam giác cân)
hay AM=AF(1)
Xét ΔCFM có
CE là đường cao ứng với cạnh MF(\(CE\perp MF\))
CE là đường trung tuyến ứng với cạnh MF(E là trung điểm của MF)
Do đó: ΔCFM cân tại C(Định lí tam giác cân)
hay CM=CF(2)
Vì ΔABC vuông tại A(gt) có AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(CM=BM=\dfrac{BC}{2}\)(M là trung điểm của BC)
nên AM=CM=BM(3)
Từ (1), (2) và (3) suy ra AM=AF=CF=CM=BM
Xét tứ giác AMCF có AM=CM=CF=FA(cmt)
nên AMCF là hình thoi(Dấu hiệu nhận biết hình thoi)
b)
Sửa đề: Tìm điều kiện của ΔABC để tứ giác AMCF là hình vuông
Hình thoi AMCF trở thành hình vuông khi \(\widehat{AMC}=90^0\)
hay \(AM\perp BC\)
Xét ΔABC có
AM là đường cao ứng với cạnh BC(\(AM\perp BC\))
AM là đường trung tuyến ứng với cạnh BC(M là trung điểm của BC)
Do đó: ΔABC cân tại A(Định lí tam giác cân)
hay AB=AC
Vậy: Khi ΔABC có thêm điều kiện AB=AC thì AMCF trở thành hình vuông
c)
Ta có: MD\(\perp\)AB(gt)
AC\(\perp\)AB(ΔABC vuông tại A)
Do đó: MD//AC(Định lí 1 từ vuông góc tới song song)
Xét ΔABC có
M là trung điểm của BC(gt)
MD//AC(cmt)
Do đó: D là trung điểm của AB(Định lí 1 đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
D là trung điểm của AB(cmt)
Do đó: MD là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
nên \(MD=\dfrac{AC}{2}\)(Định lí 2 đường trung bình của tam giác)(1)
Ta có: \(ME\perp AC\)(gt)
\(AB\perp AC\)(ΔABC vuông tại A)
Do đó: ME//AB(Định lí 1 từ vuông góc tới song song)
Xét ΔABC có
M là trung điểm của BC(gt)
ME//AB(cmt)
Do đó: E là trung điểm của AC(Định lí 1 đường trung bình của tam giác)
nên \(CE=\dfrac{AC}{2}\)(2)
Từ (1) và (2) suy ra MD=CE
Xét tứ giác CMDE có
MD//CE(MD//AC)
MD=CE(cmt)
Do đó: CMDE là hình bình hành(Dấu hiệu nhận biết hình bình hành)
nên Hai đường chéo CD và EM cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà I là trung điểm của EM(gt)
nên I là trung điểm của CD(đpcm)
Cho tam giác ABC vuông tại A và M là trung điểm cạnh BC. Từ M kẻ MD vuông góc với AB (D thuộc AB) và ME vuông góc với AC (E thuộc AC)
a) Chứng minh tứ giác ADME là hình chữ nhật
b)Gọi N là điểm đối xứng với M qua E,O là giao điểm AM và DE.Chứng minh 3 điểm B,O,N thẳng hàng
c)Tam giác ABC cần điều kiện gì để tứ giác ABCN là hình thang cân
cho tam giác ABC ( góc A= 90 độ ), AM là trung tuyến. Biết AB= 6cm, AC= 8cm
a) tính độ dài cạnh BC và AM
b) từ M kẻ MD vuông góc với AB. Tứ giác ADMC là hình gì? Vì sao?
c) trên tia đối của tia DM, lấy điểm E sao cho DM = DE. Chứng minh tứ giác AEBM là hình thoi
d) tứ giác AEMC là hình gì ? vì sao?
e) gọi F là điểm đối xứng với M qua AC. Chứng tỏ rằng F đối xứng với D qua AC, F là giao điểm của DN và AC. Chứng tỏ rằng F đối xứng với E qua điểm A
Giải thích các bước giải:
ta có: Tam giác ABC vuông tại A (gt)
=> AB^2+AC^2=BC^2
6^2+8^2 =BC^2
36+64 =BC^2
100 =BC^2
=>BC=10cm
Tam giác ABC vuông tại A có Am là đg trung tuyến
=> AM=BC/2=10/2=5cm
HÌNH VẼ THÌ BẠN TỰ VẼ NHÉ, HÌNH NÀY DỄ VẼ MÀ NHỈ.
Câu a bạn V (Team BTS) làm rồi nên mình chỉ làm các câu còn lại thôi nhé.
b) Vì DM vuông góc AB, AC vuông góc AB (gt) => DM // AC.
=> DMCA là hình thang mà góc ADM = góc DAC = 90 độ.
Do đó ADMC là hình thang vuông.
c) Xét tam giác ABC ta có: DM // AC (cmt), M là trung điểm BC (AM là trung tuyến)
=> D là trung điểm của AB.
Tứ giác AEBM có AB và EM là hai đường chéo cắt nhau tại trung điểm D. => AEBM là hình bình hành. (1)
Lại xét tam giác AMB cân tại M (MA=MB) có MD là trung tuyến => MD cũng là đường cao=> ME vuông góc AB tại D. (2)
Từ (1) và (2) => AEBM là hình thoi.
d) Vì AEBM là hình thoi => AE // BM, AE = BM.
Mà BM = MC => AE // MC, AE = MC. Do đó AEMC là hình bình hành.
e, Câu e mình không hiểu lắm vì thấy đề bài cứ sai sai làm sao. Mình chỉ chứng minh câu F đối xứng với E qua A thôi nhé.
Gọi I là giao điểm của AC và MF. Vì M đối xứng F qua AC => I là trung điểm MF, AC vuông góc MF tại I.
Chứng minh tương tự câu c ta sẽ được AFMC là hình thoi => AF // MC, AF = MC.
Mà AE // MC, AE = MC (cmt)
=> A, E, F thẳng hàng (tiên đề Ơ-clit) và A là trung điểm của EF (AE=AF)
Vậy F đối xứng E qua A.