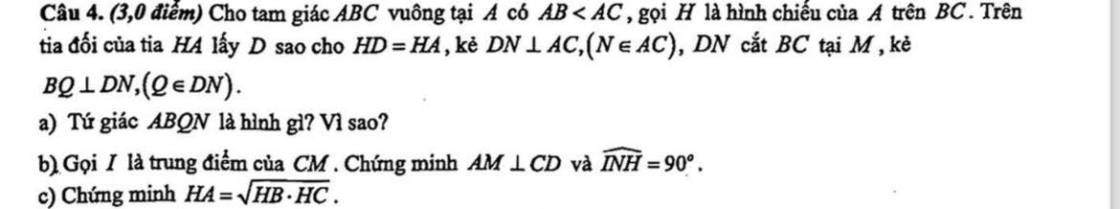Ý a,b,c cho mình xin kết quả để đối chiếu thôi ạ. Còn ý d làm rõ hộ mình. Cảm ơn nhiều ạ❤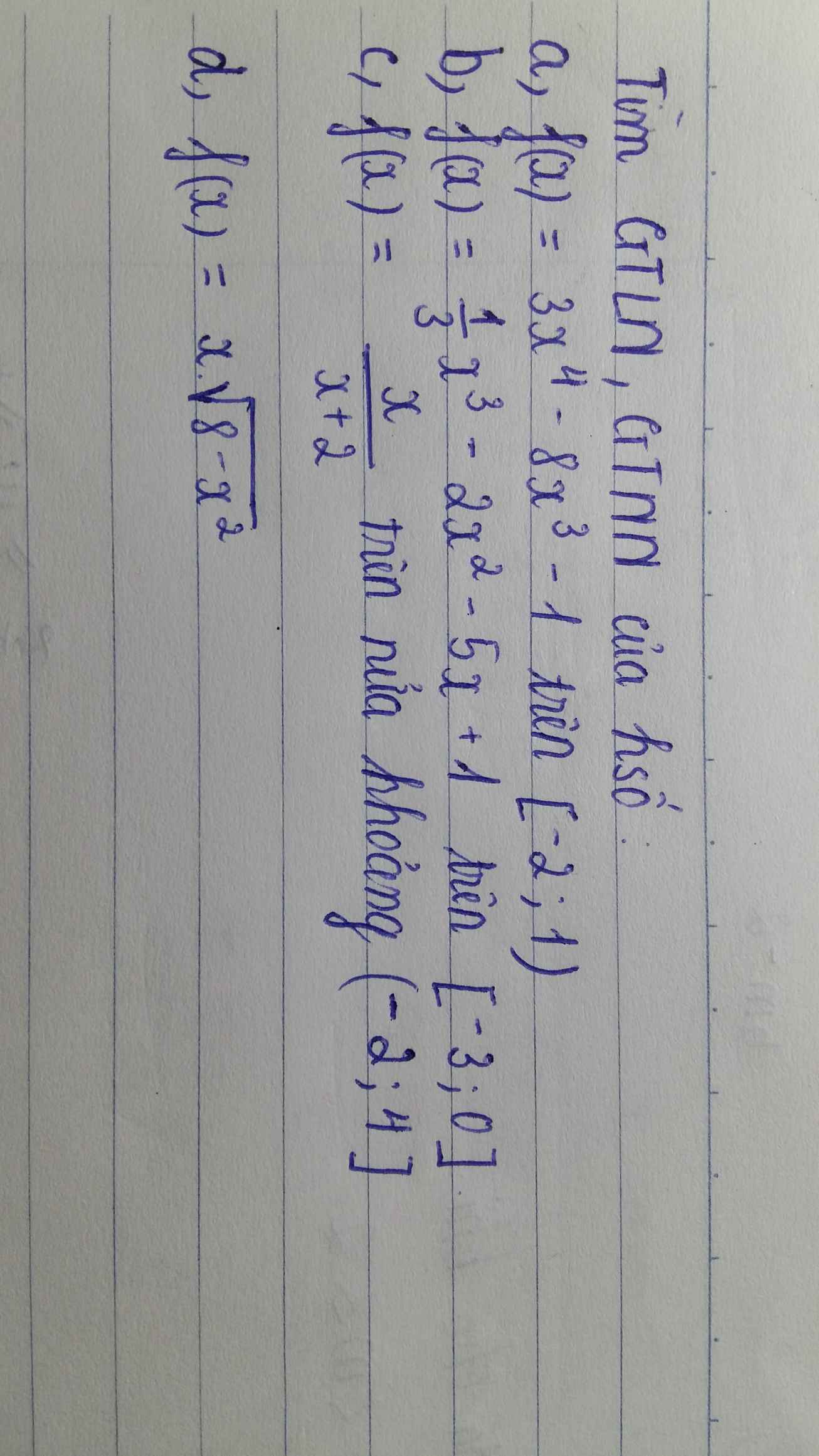

Những câu hỏi liên quan
Làm hộ mình để mình có ý tưởng với ạ xin cảm ơn nhiều.
Giải giúp mình với, mình cần gấp ạ! Không cần vẽ hình cũng đc ạ, Mình cảm ơn rất nhiều!!
Cho tam giác ABC vuông tại A, có AB = 6cm; AC = 8cm. Kẻ phân giác AD của góc A (D BC). Tính AD (làm tròn kết quả đến chữ số thập phân thứ hai).
(Gợi ý: Kẻ đường cao AH của tam giác ABC).
Mình cảm ơn mn nhiều nha . Hnay mình ms ktra Lý xòn rùi ạ. Giờ chờ kết quả thôi , nhưng mình làm bài cũng tốt . Chắc kết quả cx cao . Cảm ơn mn nhìu ![]()
![]()
Xem thêm câu trả lời
Khi miêu tả người, tài năng của Nguyễn Du còn mang theo dự cảm của cuộc đời, em hãy làm rõ ý kiến trên.
Giải giúp mình vs ạ! ❤
cho tam giác ABC cân tại A ( góc A 90 độ ). kẻ các đường vuoonggosc với AB tại B, vuông góc với AC tại C, chúng cắt nhau tại I.a. chứng minh AI là phân giác góc BAC ( đã làm )b. gọi H lafhifnh chiếu của B trên AC. chứng minh CM // BI ( M là giao điểm của AI và BH )c. tam giác ABC cần có điều kiện gì để AB2AHLưu ý: Đề đúng, giúp mình ý b và c ( có thể thì giúp mình vẽ hình với tại câu b mình k biết vẽ hình )Mình sẽ tick những ai giúp mình làm bài. giải càng chi tiết càng nhiều phần thưởng ạ. Xin...
Đọc tiếp
cho tam giác ABC cân tại A ( góc A < 90 độ ). kẻ các đường vuoonggosc với AB tại B, vuông góc với AC tại C, chúng cắt nhau tại I.
a. chứng minh AI là phân giác góc BAC ( đã làm )
b. gọi H lafhifnh chiếu của B trên AC. chứng minh CM // BI ( M là giao điểm của AI và BH )
c. tam giác ABC cần có điều kiện gì để AB=2AH
Lưu ý: Đề đúng, giúp mình ý b và c ( có thể thì giúp mình vẽ hình với tại câu b mình k biết vẽ hình )
Mình sẽ tick những ai giúp mình làm bài. giải càng chi tiết càng nhiều phần thưởng ạ.
Xin vui lòng k bình luận k liên quan đến đề nhé. Mình xin cảm ơn trước, mình mới vào nên mongmn giúp đỡ nhiều hơn
MÌNH ĐANG CẦN GẤP LẮM Ạ!!!!!
hình bạn tự vẽ nhé
a. ví tam giác ABC là tam giác cân và có góc A bằng 90 độ nên tam giác ABC là tam giác vuông cân tại A
=> góc BAC = 90 độ và AB=AC
Xét tứ giác ABIC có góc BAC =90 độ, góc ABI = 90 độ (vì AIvuông góc với AB ), góc ACI =90độ (vì AC vuông góc với CI)
=> tứ giác ABIC là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
mà AB=AC (cmt)
=> Tứ giác ABIC là hình vuông (dấu hiệu nhận biết hình vuông)
=> AI là phân giác góc BAC
mọi người có thể làm và giải thích rõ ở phần đối chiếu điều kiện với kết quả giúp mình với ạ, vì nhiều khi có kết quả mình lại không biết kết quả nào thỏa mãn ,kết quả nào loại
Đọc tiếp
mọi người có thể làm và giải thích rõ ở phần đối chiếu điều kiện với kết quả giúp mình với ạ, vì nhiều khi có kết quả mình lại không biết kết quả nào thỏa mãn ,kết quả nào loại
Bạn nào giải hộ mình 3 ý này với ạ mình cần gấp cảm ơn nhiều ạ
Câu 1:
TXĐ: D=R
\(f\left(-x\right)=2\cdot\left(-x\right)^4-3\cdot\left(-x\right)^2+1=2x^4-3x^2+1=f\left(x\right)\)
Vậy: f(x) là hàm số chẵn
Đúng 2
Bình luận (1)
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ
a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)
Đúng 1
Bình luận (3)
Cho mình hỏi bài này với ạ, làm mãi mà thấy đề sao sao ý ạ
Cho |a| < 1, |b-1|<10, |a-c| <10. Chứng minh: |a.b - c|< 20.
xin cảm ơn ạ
có \(\left|a\right|< 1\),\(\left|b-1\right|< 10\)suy ra \(\left|a\right|.\left|b-1\right|< 10\Rightarrow\left|a\left(b-1\right)\right|< 10\Leftrightarrow\left|ab-a\right|< 10\)
\(\Leftrightarrow-10< ab-a< 10\)(1)
có \(\left|a-c\right|< 10\Leftrightarrow-10< a-c< 10\)(2)
cộng lần lượt các vế của (1) và (2) ta có \(-10+\left(-10\right)< ab-a+a-c< 10+10\Leftrightarrow-20< ab-c< 20\)
suy ra \(\left|ab-c\right|< 20\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời