Giải dùm em bài toán so sánh : 231 và 321

Những câu hỏi liên quan
So sánh: 3 21 va 2 31
giải dùm em bài toán hình ạ, em đang cần gấp ;-;
ai biết thì giải dùm mk bài so sánh này nhé: 11/54 và 22/37
ta thấy:11/54=22/108
vì 108> 37
=> 22/108< 22/37
hay 11/54< 22/37
Đúng 0
Bình luận (0)
\(Tacó:\frac{11}{54}=\frac{11.37}{54.37}=\frac{407}{1998}\)
\(\frac{22}{37}=\frac{22.54}{37.54}=\frac{1188}{1998}\)
\(\frac{407}{1998}<\frac{1188}{1998}\Rightarrow\frac{11}{54}<\frac{22}{47}\)
Đúng 0
Bình luận (0)
các bạn giải hộ giùm mình bài toán này nhé !!!!
so sánh:
2^225 và 3^150
Ta có:
2225 = (29)25 = 51225
3150 = (36)25 = 72925
Vì 51225 < 72925 => 2225 < 3150
Đúng 0
Bình luận (0)
cách anh chị giải hộ em bài toán này hãy so sánh 360 và 935
\(9^{35}=\left(3^2\right)^{35}=3^{70}\)
VÌ \(3^{60}< 3^{70}\)
NÊN \(3^{60}< 9^{35}\)
Đúng 0
Bình luận (0)
Ta có :
\(9^{35}=\left(3^2\right)^{35}=3^{70}\)
Vì \(3^{60}< 3^{70}\Rightarrow3^{60}< 9^{35}\)
Vậy\(3^{60}< 9^{35}\)
Đúng 0
Bình luận (0)
935 = (32)35= 370
Ta thấy 360< 370 => 360< 935
Vậy 360< 935
Đúng 0
Bình luận (0)
So sánh 2 ps 932/1023 và ps 876/997
em hãy giải bài toán sau ko đc quy đồng, đảo ngược ps
Ta có:
\(\frac{932}{1023}=1-\frac{91}{1023}\)
\(\frac{876}{997}=1-\frac{121}{997}\)
Ta thấy: \(\frac{121}{997}>\frac{91}{997}>\frac{91}{1023}\)
\(\Rightarrow1-\frac{91}{1023}>1-\frac{121}{997}\)
\(\Rightarrow\frac{932}{1023}>\frac{876}{997}\)
Đúng 0
Bình luận (0)
so sánh giùm mik bài này cái
321 và 231
\(3^{21}=3^{20}.3=9^{10}.3\)
\(2^{31}=2^{30}.2=8^{10}.2\)
Do \(9^{10}>8^{10},3>2\)
\(\Rightarrow9^{10}.3>8^{10}.2\Rightarrow3^{21}>2^{31}\)
Đúng 1
Bình luận (0)
\(3^{21}=3^{20}\cdot3\)
\(2^{31}=2^{30}\cdot2\)
mà \(3^{20}>2^{30}\)
nên \(3^{21}>2^{31}\)
Đúng 1
Bình luận (0)
Giải phương trình nhận được rồi suy ra đáp số của bài toán. So sánh hai cách chọn ẩn, em thấy cách nào cho lời giải gọn hơn?
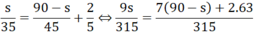
⇔ 9s = 7(90 - s) + 126
⇔ 9s = 756 - 7s
⇔ 16s = 756
⇔ s = 47,25(km)
Thời gian để hai xe gặp nhau từ lúc xe máy khởi hành là:
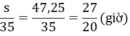
So sánh hai cách chọn ẩn, cách đầu tiên (chọn ẩn là thời gian từ lúc xe máy khởi hành đến lúc hai xe gặp nhau) cho cách giải ngắn gọn hơn vì phương trình đơn giản hơn.
Đúng 0
Bình luận (0)
Giúp tôi giải bài toán sau: Hãy so sánh 2a và a2?
2a=a2 trong mọi trường hợp a khác 2 và -2
Đúng 0
Bình luận (0)
Ta thấy :
2a=a+a (1)
a^2=a.a (2)
Từ (1) và (2);ta có:
a.a > a+a
Nên a^2 > 2a
Đúng 0
Bình luận (0)




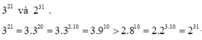







![[A]ȵȟ•βê•ʠǔá♡](https://hoc24.vn/images/avt/avt1063100_256by256.jpg)











