Tính thể tích vật thể :
a) Có đáy là một tam giác cho bởi \(y=x;y=0;x=1\).Mỗi thiết diện vuông góc với trục Ox là một hình vuông
b) Có đáy là một hình tròn giới hạn bởi \(x^2+y^2=1\). Mỗi thiết diện vuông góc với trục Ox là một hình vuông
Tính thể tích vật thể:
a) Có đáy là một tam giác cho bởi: y = x , y = 0 , và x = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông.
b) Có đáy là một hình tròn giới hạn bởi x 2 + y 2 = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông.
a) Đáp số: 1/3.
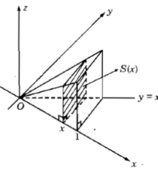
Hướng dẫn: Hình chóp (H.82). Thiết diện tại x ∈ [0;1] là hình vuông cạnh bằng x, S(x) = x 2 .
Vậy
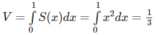
b) Đáp số: 16/3.
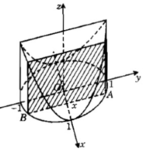
Hướng dẫn: (H.83) Thiết diện tại x ∈ [-1;1] là hình vuông cạnh AB, trong đó A(x; y)
với 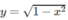
Khi đó, 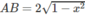
Diện tích thiết diện là: S(x) = 4(1 − x 2 ).
Vậy
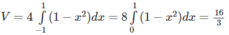
Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1 (hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x − 1 ≤ x ≤ 1 thì được thiết diện là một tam giác đều. Tính thể tích V của vật thể đó

A. V = 3
B. V = 3 3
C. V = 4 3 3
D. V = π
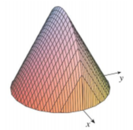
Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1 (hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x - 1 ≤ x ≤ 1 thì được thiết diện là một tam giác đều. Tính thể tích V của vật thể đó
A. V = 3
B. V = 3 3
C. V = 4 3 3
D. V = π
Cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x thì được thiết diện là một tam giác đều cạnh
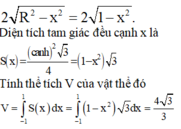
Đáp án C
Cho phần vật thể A giới hạn bởi hai mặt phẳng x = 0 ; x = 1 cắt phần vật thể B bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 1 ta được thiết diện là một tam giác đều có độ dài canh bằng x 1 − x . Tính thể tích phần vật thể B.
A. 3 4
B. 3 48
C. 3 6
D. 3 12
Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình x=0 và x=2. Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x, ta được thiết diện là một tam giác đều có độ dài cạnh bằng x 2 - x . Tính thể tích V của phần vật thể (T).
![]()

![]()
![]()
Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = 2. Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 2 , , ta được thiết diện là một tam giác đều có độ dài cạnh bằng x 2 − x . Tính thể tích V của phần vật thể (T).
A. V = 4 3 .
B. V = 3 3 .
C. V = 4 3 .
D. V = 3 .
Đáp án B
V = ∫ 0 2 1 2 . x . 2 − x . 3 2 . x . 2 − x d x = 3 4 ∫ 0 2 x 2 ( 2 − x ) d x = 3 3
Cho phần vật thể ξ giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = 2. Cắt phần vật thể ξ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 2 , ta được thiết diện là một tam giác đều có độ dài cạnh x 2 − x . Tính thể tích V của phần vật thể ξ
A. V = 4 3
B. V = 3 3
C. V = 4 3
D. V = 3
Đáp án B
Diện tích tam giác đều cạnh x 2 − x là S x = 3 4 x 2 2 − x
Vậy thể tích cần tính là V = ∫ 0 2 S x d x = 3 4 ∫ 0 2 2 x 2 − x 3 d x = 3 4 . 4 3 = 3 3
Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = 2 Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ 0 ≤ x ≤ 2 , ta được thiết diện là một tam giác đều có độ dài cạnh bằng x 2 - x . Tính thể tích V của phần vật thể (T).
A. V = 4 3 .
B. V = 3 3 .
C. V = 4 3 .
D. V = 3 .
Tính thể tích vật thể giới hạn bởi hai mặt phẳng x = 0 , x = π . Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác vuông cân có cạnh huyền bằng sin x + 2 .
A. ![]()
B. ![]()
C. ![]()
D. ![]()