Cho tình hình ABCD có AB = 3a; AD = 5a. Góc BAD bằng \(120^0\) :
a) Tìm các tích vô hướng sau : \(\overrightarrow{AB}.\overrightarrow{AD};\overrightarrow{AC}.\overrightarrow{BD}\)
b) Tính độ dài BD và bán kính đường tròn ngoại tiếp tam giác ABC
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB 2a; BC = \(\dfrac{3a}{2}\); AD = 3a. Hình chiếu vuông góc của S lên (ABCD) l;à trung điểm H của BD. Biết góc giữa (SCD) và (ABCD) bằng 60 độ. Tình khoảng cách từ C đến (SBD)?
Ta có
\(SH\perp\left(ABCD\right);SH\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(ABCD\right)\)
Trong mp (ABCD) từ C dựng đường thẳng vuông góc với BD cắt BD tại F ta có
\(SH\perp\left(ABCD\right);CF\in ABCD\Rightarrow SH\perp CF\)
Mà \(CF\perp BD\)
Ta có \(BD\in\left(SBD\right);SH\in\left(SBD\right)\)
\(\Rightarrow CF\perp\left(SBD\right)\) => CF là khoảng cách từ C đến (SBD)
Trong mp (ABCD) nối CH cắt AD tại E
Ta có BC//AD \(\Rightarrow\dfrac{BC}{ED}=\dfrac{HB}{HD}=\dfrac{HC}{HE}=1\Rightarrow ED=BC=\dfrac{3a}{2}\)
\(\Rightarrow EA=AD-ED=3a-\dfrac{3a}{2}=\dfrac{3a}{2}=BC\)
Mà BC//AE và \(\widehat{ABC}=90^o\)
=> ABCE là hình chữ nhật
Trong mp (ABCD) từ H dựng đường thẳng vuông góc với CD cắt CD tại K
Xét tg vuông CDE có
\(CD=\sqrt{CE^2+ED^2}=\sqrt{4a^2+\dfrac{9a^2}{4}}=\dfrac{5a}{2}\)
Xét tg vuông ABD có
\(BD=\sqrt{AB^2+AD^2}=\sqrt{4a^2+9a^2}=a\sqrt{13}\)
\(\Rightarrow HB=HD=\dfrac{BD}{2}=\dfrac{a\sqrt{13}}{2}\)
Xét tg vuông CKH và tg vuông CED có \(\widehat{ECD}\) chung
=> tg CKH đồng dạng với tg CED (g.g.g)
\(\Rightarrow\dfrac{CK}{CE}=\dfrac{HC}{CD}\Rightarrow CK=\dfrac{CE.HC}{CD}=\dfrac{2a.a}{\dfrac{5a}{2}}=\dfrac{4a}{5}\)
Xét tg vuông CKH có
\(HK=\sqrt{HC^2-CK^2}=\sqrt{a^2-\dfrac{16a^2}{25}}=\dfrac{3a}{5}\)
Xét tg vuông DKH và tg vuông DFC có \(\widehat{BDC}\) chung
=> tg DKH đồng dạng với tg DFC (g.g.g)
\(\Rightarrow\dfrac{HK}{CF}=\dfrac{HD}{CD}\Rightarrow CF=\dfrac{HK.CD}{HD}=\dfrac{\dfrac{3a}{5}.\dfrac{5a}{2}}{\dfrac{a\sqrt{13}}{2}}=\dfrac{3a\sqrt{13}}{13}\)
Cho hình chữ nhật ABCD có AB = 3a, BC = 4a.Tính độ dài vecto AB + vecto AD
\(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=AC=5a\)
Cho hình chóp S.ABCD có S A ⊥ A B C D và ABCD là hình chữ nhật với AB=a, A C = a 5 , S C = 3 a . Tính thể tích hình chóp S.ABCD
A. 4 a 3
B. 4 a 3 3
C. 2 a 3 3
D. a 3 3
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật. Tính thể tích S.ABCD biết A B = a ; A D = 2 a ; S A = 3 a .
A. a 3
B. 6 a 3
C. 2 a 3
D. a 3 3
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và ABCD là hình chữ nhật với AB=a, AC=a 5 , SC=3a. Tính thể tích hình chóp S.ABCD
A. 4 a 3
B. 4 a 3 3
C. 2 a 3 3
D. a 3 3
Đáp án là B
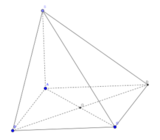
Tam giác ABC vuông tại B nên
![]()
Tam giác SAC vuông tại A nên
![]()
Thể tích hình chóp S.ABCD là
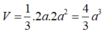
cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a , SA=3a và SA vuông góc với (ABCD). Tính góc giữa SD và mặt phẳng ABCD
(SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=3/2
=>góc SDA=56 độ
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a, SA = 3a. Biết SA vuông góc với mặt phẳng (ABCD). Thể tích khối chóp S.ABCD là:
A. a 3
B. 2 a 3
C. 6 a 3
D. 12 a 3
Cho hình chóp S.ABCD có đáy (ABCD) là hình chữ nhật, cạnh bên SA vuông góc với đáy (ABCD). Biết AB=a, BC=2a và SC=3a . Tính thể tích khối chóp S.ABCD?
A. 2 a 3
B. a 3
C. 4 3 a 3
D. 2 5 3 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy (ABCD). Biết AB=a, BC=3a, SA=2a.Tính thể tích V của khối chóp S.ABCD.
A. V = 3 a 3
B. V = 2 a 3
C. V = a 3
D. V = 6 a 3
Đáp án B
Thể tích khối chóp S.ABCD là:
V A B C D = 1 3 S A . S A B C D = 1 3 2 a .3 a 2 = 2 a 3