Tìm tất cả giá trị của tham số m để đồ thị hàm số y=\(\dfrac{x^2-1}{x^2+2mx-m}\) có 3 tiệm cận

Những câu hỏi liên quan
tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y=\dfrac{5x-3}{x^2-2mx+1}\) không có tiệm cận đứng .
Do mẫu có bậc 2 còn tử bậc 1 \(\Rightarrow\)hàm không có tiệm cận đứng khi và chỉ khi phương trình \(x^2-2mx+1=0\) vô nghiệm
\(\Leftrightarrow\Delta'=m^2-1< 0\)
\(\Rightarrow-1< m< 1\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số
y
x
−
1
+
2017
x
2
−
2
m
x
+
m
+
2
đúng 3 đường tiệm cận? A.
2...
Đọc tiếp
Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số y = x − 1 + 2017 x 2 − 2 m x + m + 2 đúng 3 đường tiệm cận?
A. 2 < m ≤ 3
B. 2 ≤ m ≤ 3
C. m < 2
D. m > 2 hoặc m < − 1
Đáp án A
Ta có: lim x → + ∞ y = 0 ⇒ đồ thị hàm số có 1 tiệm cận ngang là y = 0 .
Để đồ thị hàm số có 3 tiệm cận thì phương trình : g x = x 2 − 2 m x + m + 2 = 0 có 2 nghiệm phân biệt
x 1 > x 2 ⇔ Δ ' = m 2 − m − 2 > 0 x 1 − 1 x 2 − 1 ≥ 0 x 1 − 1 + x 2 − 1 > 0 ⇔ m + 1 m − 2 > 0 x 1 x 2 − x 1 + x 2 + 1 ≥ 0 x 2 + x 2 > 2 ⇔ m + 1 m − 2 > 0 m + 2 − 2 m + 1 > 0 2 m > 2 ⇔ 3 ≥ m > 2.
Đúng 0
Bình luận (0)
Cho hàm số
y
1
-
x
x
2
-
2
m
x
+
4
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba đường tiệm cận? A.
m
2...
Đọc tiếp
Cho hàm số y = 1 - x x 2 - 2 m x + 4 . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba đường tiệm cận?
A. m > 2 h ặ c m < - 2 m ≠ 5 2
B. m > 2 m ≠ 5 2
C. - 2 < m < 2
D. m<-2 hoặc m>2
Cho hàm số
y
1
-
x
x
2
-
2
m
x
+
4
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba đường tiệm cận
Đọc tiếp
Cho hàm số y = 1 - x x 2 - 2 m x + 4 . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba đường tiệm cận
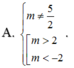
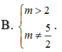
![]()
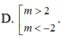
Cho hàm số
y
1
-
x
x
2
-
2
m
x
+
4
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba đường tiệm cận A.
m...
Đọc tiếp
Cho hàm số y = 1 - x x 2 - 2 m x + 4 . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba đường tiệm cận
A. m > 2 m < - 2 m ≠ 5 2
B. m > 2 m ≠ 5 2
C. -2<m<2
D. m < - 2 m > 2
Cho hàm số
y
1
x
2
-
2
m
+
1
x
+
2
m
x
-...
Đọc tiếp
Cho hàm số
y = 1 x 2 - 2 m + 1 x + 2 m x - m . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có 4 đường tiệm cận
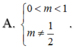
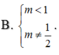
![]()
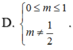
Tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
2
-
1
x
2
+
2
m
x
-
m
có 3 tiệm cận là. A.
m
∈
ℝ
1
;...
Đọc tiếp
Tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 2 - 1 x 2 + 2 m x - m có 3 tiệm cận là.
A. m ∈ ℝ \ 1 ; 1 3
B. m ∈ - ∞ ; - 1 ∪ 0 ; + ∞
C. m ∈ - 1 ; 0 \ - 1 3
D. m ∈ - ∞ ; - 1 ∪ 0 ; + ∞ \ 1 3
Chọn D.
Phương pháp: Sử dụng định nghĩa đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số.
![]()
Dễ thấy đồ thị hàm số có một tiệm cận ngang y = 1.
Để đồ thị hàm số có ba đường tiệm cận thì đồ thị hàm số phải có hai tiệm cận đứng.
Điều kiện cần và đủ để đồ thị hàm số đã cho có hai tiệm cận đứng là mẫu số có hai nghiệm phân biệt không là nghiệm của tử số.
Hay
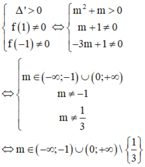
Đúng 0
Bình luận (0)
Tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
2
-
1
x
2
+
2
m
x
-
m
có 3 tiệm cận là A.
m
∈
ℝ
1...
Đọc tiếp
Tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 2 - 1 x 2 + 2 m x - m có 3 tiệm cận là
A. m ∈ ℝ \ 1 ; 1 3
B. m ∈ - ∞ ; - 1 ∪ 0 ; + ∞
C. m ∈ - 1 ; 0 \ - 1 3
D. m ∈ - ∞ ; - 1 ∪ 0 ; + ∞ \ 1 3
tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y=\dfrac{x+1}{\sqrt{mx^2+1}}\) có 2 tiệm cận ngang.
Với \(m=0\) ko thỏa mãn
Với \(m\ne0\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=-\dfrac{1}{\sqrt{m}}\); \(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=\dfrac{1}{\sqrt{m}}\)
\(\Rightarrow\) Hàm có 2 TCN khi \(\sqrt{m}\) xác định \(\Rightarrow m>0\)
Đúng 1
Bình luận (0)
Tìm tất cả giá trị của tham số m để đồ thị hàm số
y
x
-
m
x
2
-
(
m
+
1
)
x
+
m
có hai tiệm cận A.
m
≠
1
B.
m
≥...
Đọc tiếp
Tìm tất cả giá trị của tham số m để đồ thị hàm số y = x - m x 2 - ( m + 1 ) x + m có hai tiệm cận
A. m ≠ 1
B. m ≥ 1
C. m ≤ 1
D. m ∈ ℝ













