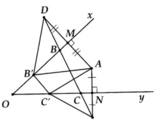
Cho tam giác ABC nhọn. Tìm điểm M nằm trong sao cho AM+BM+CM nhỏ nhất

Những câu hỏi liên quan
Cho tam giác ABC nhọn. Tìm điểm M nằm trong sao cho AM+BM+CM nhỏ nhất
trên nửa mặt phẳng bờ AM chứa điểm C vẽ tam giác đều AMN => MA=MN (1)
Vẽ ra ngoài tam giác ABC tam giác đều ACP
Bạn tự đi chứng minh tam giác AMC = tam giác ANP
=> MC=NP (2)
Từ (1) và (2) => MA+MB+MC=BM+MN+NP \(\ge\)BP (theo tính chất đường gấp khúc)
Dấu = xảy ra \(\Leftrightarrow\)B,M,N,P thẳng hàng
\(\Leftrightarrow\)Góc AMB = Góc ANP =120 độ (vì AMN=ANM=60 độ)
\(\Leftrightarrow\)AMB=AMC=120 (vì 2 tam giác chứng minh trên bằng nhau nên 2 góc AMC và ANP bằng nhau)
\(\Leftrightarrow\)AMB=AMC=BMC=120
chỉ cần đến đây thôi nhé
Đúng 0
Bình luận (0)
Cho điểm A nằm trong góc nhọn xOy.
a) Tìm hai điểm M, N thuộc Ox và Oy sao cho AM + AN là nhỏ nhất.
b) Tìm hai điểm B, C thuộc Ox và Oy sao cho tam giác ABC có chu vi nhỏ nhất
a, Cho 2 điểm A và B cùng nằm trong nửa mặt phẳng có bờ là đường thẳng xy. Tìm trên xy điểm M sao cho AM + BM bé nhất.
b, Cho góc nhọn xOy và điểm A nằm trong góc đó. Tìm điểm B trên Ox và điểm C trên Oy sao cho chu vi của tam giác ABC bé nhất.
Cho tam giác đều ABC, lấy điểm M nằm trong tam giác sao cho AM=1, BM=2; CM =căn bậc 2 của 3
cho tam giác ABC, điểm M nằm trong tam giác ABC. CM AM+BM+CM<AB+BC+AC
Help me!
Cho tam giác ABC đều. M là một điểm nằm trong tam giác. Lấy điểm D, E, F lần lượt thuộc AC, AB, BC sao cho DE=AM, DF=CM, EF=BM. Xác định vị trí của M để diện tích tam giác DEF đạt giá trị lớn nhất.
cho tam giác ABC nhọn. tìm vị trí điểm D nằm trong tam giác sao cho DA+DB+DC nhỏ nhất.
1/ Cho hình vuông ABCD. Lấy M tùy ý trên cạnh BC. Đường thẳng vuông góc AM tại M, cắt CD tại N. Tìm vị trí của M để CN lớn nhất2/ Cho hình vuông ABCD. Lấy M,N,P,Q thuộc 4 cạnh AB,BC,CD,AD. TÌm điều kiện của tứ giác MNPQ để chu vi tứ giác MNPQ nhỏ nhất3/ Lấy I nằm trong tam giác ABC nhọn. Vẽ IH⊥BC,IK⊥AC,IL⊥AB. Xác định vị trí của I để AL^2+BH^2+CK^2 nhỏ nhất4/ Cho tam giác ABC nhọn. Tìm điểm M trong tam giác sao cho AM.BC+BM.AC+CM.AB nhỏ nhất
Đọc tiếp
1/ Cho hình vuông ABCD. Lấy M tùy ý trên cạnh BC. Đường thẳng vuông góc AM tại M, cắt CD tại N. Tìm vị trí của M để CN lớn nhất
2/ Cho hình vuông ABCD. Lấy M,N,P,Q thuộc 4 cạnh AB,BC,CD,AD. TÌm điều kiện của tứ giác MNPQ để chu vi tứ giác MNPQ nhỏ nhất
3/ Lấy I nằm trong tam giác ABC nhọn. Vẽ \(IH⊥BC,IK⊥AC,IL⊥AB\). Xác định vị trí của I để \(AL^2+BH^2+CK^2\) nhỏ nhất
4/ Cho tam giác ABC nhọn. Tìm điểm M trong tam giác sao cho AM.BC+BM.AC+CM.AB nhỏ nhất
cho tam giác nhọn ABC gọi M là điểm bất kỳ nằm trong tam giác AM cắt BC tại D BM cắt AC tại E CM cắt AB tại F
cm : AM/AD +BM/BE +CM/CF =2