Cho hình bình hành ABCD có \(A\left(-1;-2\right);B\left(3;2\right);C\left(4;-1\right)\). Tìm tọa độ đỉnh D ?

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD có \(A\left(1;-2\right);B\left(3;2\right);C\left(-4;1\right)\). Tìm tọa độ đỉnh D ?
Gọi điểm D(x,y) là điểm cần tìm.
Tứ giác ABCD là hình bình hành khi và chỉ khi: \(\overrightarrow{AB}=\overrightarrow{DC}\).
\(\overrightarrow{AB}\left(2;4\right)\); \(\overrightarrow{DC}\left(-4-x;1-y\right)\).
\(\overrightarrow{AB}=\overrightarrow{DC}\)\(\Leftrightarrow\left\{{}\begin{matrix}-4-x=2\\1-y=4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=-3\end{matrix}\right.\)\(\Leftrightarrow D\left(-6;-3\right)\).
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có cạnh AB=15,1 cm AB=AD và A=60 độ . Tính S phần không chung nhau giữa hình bình hành ABCD và hình tròn nội tiếp hình bình hành ABCD
bạn kiếm câu này ở đâu z mình đang luyện thi toán casio mà câu này khó quá bạn có biết chỉ mình
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có A =90, biết AB=3cm, AC=5cm.Khi đó diện tích hình bình hành ABCD là ?
hình bình hành ABCD là hình chữ nhật( vì có 1 góc vuông)
Diện tích hình chữ nhật ABCD là
S= AB *AC= 3*5= 15 cm vuông
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có BD vuông góc với BC. Biết AB=a, góc A = α . Tính diện tích hình bình hành ABCD theo a và α
Cho hình bình hành ABCD có
A
^
120
0
, các góc còn lại của hình bình hành là? A.
B
^
60
0
,
C
^
120
0
,
D
^
60
0
B.
B
^...
Đọc tiếp
Cho hình bình hành ABCD có A ^ = 120 0 , các góc còn lại của hình bình hành là?
A. B ^ = 60 0 , C ^ = 120 0 , D ^ = 60 0
B. B ^ = 90 0 , C ^ = 120 0 , D ^ = 60 0
C. B ^ = 60 0 , C ^ = 120 0 , D ^ = 75 0
D. B ^ = 60 0 , C ^ = 45 0 , D ^ = 60 0

Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
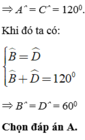
Đúng 0
Bình luận (0)
Cho HÌnh bình hành ABCD , góc ADC=1/2 góc D. Gọi M là trung điểm của AB. 2 tia DA và CM cắt nhau tại E
a) Chứng Minh: tứ giác AEBC là hình bình hành
b) Hình bình hành ABCD phải có thêm điều kiện gì để hình bình hành AEBC là hình chữ nhật
Cho tam giác ABC có \(A\left(-5;6\right):B\left(-4;-1\right);C\left(4;3\right)\). Tìm tọa độ trung điểm I của AC. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành ?
- Tìm tọa độ điểm I.
\(x_I=\dfrac{x_A+x_C}{2}=\dfrac{-1}{2}\); \(y_I=\dfrac{y_A+y_C}{2}=\dfrac{9}{2}\).
Vậy \(I\left(-\dfrac{1}{2};\dfrac{9}{2}\right)\).
- Tìm tọa độ điểm D.
Gọi \(D\left(x;y\right)\)
Tứ giác ABCD là hình bình hành \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\).
\(\overrightarrow{AB}=\left(1;-7\right)\); \(\overrightarrow{DC}=\left(4-x;3-y\right)\).
Do \(\overrightarrow{AB}=\overrightarrow{DC}\) nên:
\(\left\{{}\begin{matrix}4-x=1\\3-y=-7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-10\end{matrix}\right.\).
Vậy \(D\left(3;-10\right)\).
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. Biết \(A\left(2;-3\right);B\left(4;5\right);C\left(0;-1\right)\). Tính tọa độ của đỉnh D ?
Gọi D(x;y).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
\(\overrightarrow{AB}\left(2;8\right);\overrightarrow{DC}\left(-x;-1-y\right)\).
Do \(\overrightarrow{AB}=\overrightarrow{DC}\) nên \(\left\{{}\begin{matrix}-x=2\\-1-y=8\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-9\end{matrix}\right.\).
Vậy \(D\left(-2;-9\right)\).
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có độ dài cạnh AB là a,cạnh BC là b,Cạnh a=8cm,Cạnh b=3cm.Tính Chu vi và diện tích hình bình hành ABCD?















