cho (P ):y=-x2+x-3
a. viết phương trình tiếp tuyến ( T)và (T' ) với ( P)tại cái điêm M(0;-3 ) và N( 3;0).
b. tính diện tích giới hạn bởi ( P) và hai tiếp tuyến.
Trong mặt phẳng Oxy, cho I(-1;2), M(-3;5).
a) Viết phương trình đường tròn (C) có tâm I và đi qua M.
b) Tìm m để đường thẳng (\(\Delta\)): 2x + 3y + m = 0 tiếp xúc với (C).
c) Viết phương trình tiếp tuyến của (C) tại 2 giao điểm A, B của (C) và (d): x - 5y - 2 = 0.
d) Tìm điểm C để tam giác ABC vuông và nội tiếp (C).
b, \(d\left(I;\Delta\right)=R\Leftrightarrow\dfrac{\left|-2+6+m\right|}{\sqrt{13}}=\sqrt{13}\)
\(\Rightarrow\left[{}\begin{matrix}m=9\\m=-17\end{matrix}\right.\)
c, Dễ tìm được tọa độ A, B: \(\left\{{}\begin{matrix}A=\left(-3,-1\right)\\B=\left(2,0\right)\end{matrix}\right.\)
Phương trình tiếp tuyến tại A có dạng: \(\Delta_1:ax+by+3a+b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I,\Delta_1\right)=\dfrac{\left|-a+2b+3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{13}\)
\(\Leftrightarrow\left(2a+3b\right)^2=13a^2+13b^2\)
\(\Leftrightarrow4a^2+9b^2+12ab=13a^2+13b^2\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow3a=2b\)
\(\Rightarrow\Delta_1:2x+3y+9=0\)
Tương tự tiếp tuyến tại B: \(\Delta_2:3x-2y-6=0\)
a, \(R=IM=\sqrt{\left(-3+1\right)^2+\left(5-2\right)^2}=\sqrt{13}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=13\)
Cho hàm số y = x ln x + 1 có đồ thị (C). Viết phương trình tiếp tuyến với đồ thị (C) tại điểm có hoành độ x 0 = 2 e
A. y = 2 + ln 2 x - 2 e - 1
B. y = 2 + ln 2 x + 2 e + 1
C. y = - 2 + ln 2 x - 2 e + 1
D. y = 2 + ln 2 x - 2 e + 1
Cho hàm số y = 1 3 x 3 + x 2 - 2 có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y" = 0 là:
A. y = - x - 7 3
B. y = - x + 7 3
C. y = x - 7 3
D. y = 7 3 x
Ta có y ' = x 2 + 2 x và y" = 2x + 2.
- Theo giả thiết x 0 là nghiệm của phương trình y " ( x 0 ) = 0 .
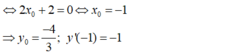
- Phương trình tiếp tuyến tại điểm 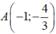 là:
là:
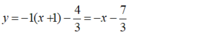
Chọn A.
Cho hàm số y = 1 3 x 3 + x 2 - 2 có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y" = 0 là:
A. y = - x - 7 3
B. y = - x + 7 3
C. y = x - 7 3
D. y = 7 3 x
- Ta có :
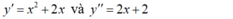
- Theo giả thiết x 0 là nghiệm của phương trình:
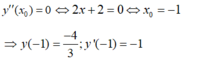
- Phương trình tiếp tuyến tại điểm 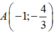 là:
là:
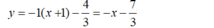
Chọn A.
Phương trình tiếp tuyến với đồ thị C 1 của hàm số y = x 3 - 1 tại giao điểm của đồ thị C 1 với
trục hoành có phương trình
A. y = 3 x - 1
B. y = 3 x - 3
C. y = 0
D. y = 3 x - 4
Bài 1. Cho hai đường tròn \(\left(C_1\right):x^2+y^2-10x=0\) và \(\left(C_2\right):x^2+y^2+4x-2y-20=0\) .
1/ Tìm tâm và bán kính của 2 đường tròn
2/ Xét vị trí tương đối của 2 đường tròn
3/ Viết phương trình tiếp tuyến chung của 2 đường tròn
1.
\(\left(C_1\right):\left(x-5\right)^2+y^2=25\Rightarrow\) Tâm \(I_1=\left(5;0\right);R_1=5\)
\(\left(C_2\right):\left(x+2\right)^2+\left(y-1\right)^2=25\Rightarrow\) Tâm \(I_2=\left(-2;1\right);R_2=5\)
2.
\(I_1I_2=\sqrt{\left(-2-5\right)^2+\left(1-0\right)^2}=5\sqrt{2}>R_1\)
\(\Rightarrow\) 2 đường tròn ngoài nhau
1.Từ điểm A ở ngoài đtròn (O) vẽ 2 tiếp tuyến AB và AC với đường tròn(O). Gọi M là trung điểm AB. Nối CM cắt đường tròn(O) tại E. AO cắt BC tại H. Tia AE cắt đường tròn (O) tại D
a. Chứng Minh MB bình=ME.MC và CD//AB
b. Vẽ OK vuông góc với ED tại K. Vẽ dây cung EN vuông góc với CK (N thuộc (O)). Cm B,O,N thẳng hàng
2.Cho điểm M nằm ngoài đtròn (O). Vẽ 2 tiếp tuyến MA,MB với đtròn. Vẽ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D), OM cắt AB và (O) lần lượt tại H và I.
a. Cm tg MAOB nội tiếp
b. Cm OH.OM+MC.MD=MO bình
c. Cm CI là tia pg của góc MCH
3. Từ điểm M nằm ngoài (O;R), vẽ 2 tiếp tuyến MA,MB và cát tuyến MCD với (O) (A,B là tiếp điểm và cát tuyến MCD nằm trong góc AMO, MC<MD). Gọi H là giao điểm của AB và OM
a) Cm tg MAOB nội tiếp, OM vuông góc AB
b) Cm AC.BD=AD.BC
cho (O;R), đường kính AB. vẽ các tiếp tuyến xx' và yy' vuông góc AB thứ tự tại A và B. Gọi M là một điểm bất kì trên cung AB (M khác A,B). Tiếp tuyến với (O;R) tại M cắt xx',yy' lần lượt tại C, D. trên nửa mặt phẳng bờ AB không chứa M dựng đường thẳng tiếp xúc với (O;R) tại N và // với CD cắt xx' và yy' theo thứ tự tại E, F. CM : 1/AC^2 + 1/BD^2 không đổi
Cho 2 đường tròn (O,R) và (O',R') cắt nhau tại I và J (R' >R) .KẺ tiếp tuyến chung của 2 đường tròn đó , chúng cắt nhau tại A. Gọi B,C là các tiếp điểm của 2 tiếp tuyến trên với (O',R'),D là tiếp điểm của tiếp tuyến AB với (O,R) ( diểm I, B ở cùng mặt phẳng bờ là O'A). Đường thẳng AI cắt (O',R') tại M khác I. K là giao của ỊJ với BD. CMR:
AM là tiếp tuyến của đường tròn ngoại tiếp tam giác IBD
Ta có: \(OD//O'B\left(\perp AB\right)\)
\(\Rightarrow\frac{AO}{AO'}=\frac{OD}{O'B}=\frac{R}{R'}=\frac{OI}{O'M}=\frac{OI}{O'I}\)
OI cắt O’I và A, I, M thẳng hàng ( gt ) nên suy ra OI // O’M \(\Rightarrow\widehat{DOI}=\widehat{BO'M}\)
Mà \(\widehat{BDI}=\frac{1}{2}\widehat{DOI}=\frac{1}{2}\)sđ cung DI và \(\widehat{BIM}=\frac{1}{2}\widehat{BO'M}=\frac{1}{2}\)sđ cung \(BM\Rightarrow\widehat{BDI}=\widehat{BIM}\)
Nên AM là tiếp tuyến của đường tròn ngoại tiếp của tam giác BDI ( đpcm )