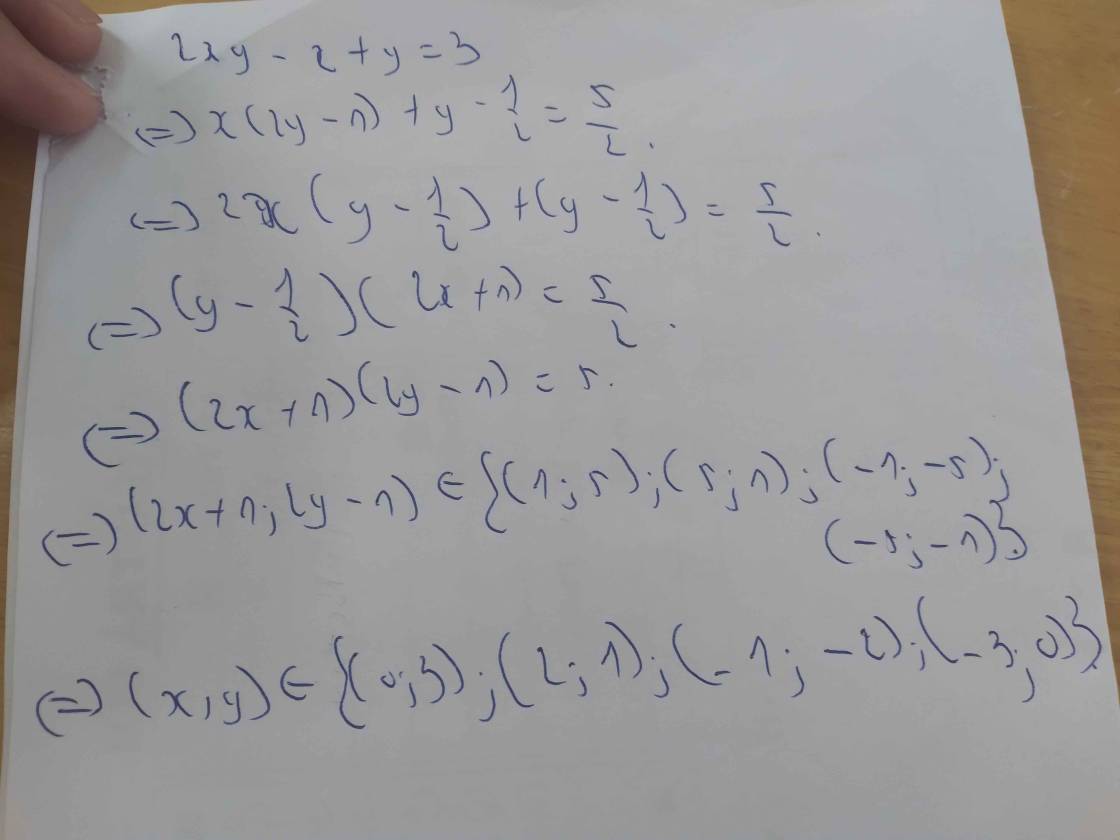Cho x,y thoã mãn : (3x-y)/(y+x) = 1/2 .Tìm x,y

Những câu hỏi liên quan
a)Cho x và y là hai số thực thoã mãn 3x-=1 chứng minh rằng : 5^2-^2<5/4
b)Cho x khác y ; x khác -y;y khác 0 thoã mãn y/x+y + 2y^2/x^2+y^2 + 4y^4/x^4+y^4 + 8y^8/x^8-y^8=2021 tính giá trị x/y
Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn. Viết đề như trên khó theo dõi quá.
Đúng 0
Bình luận (0)
Cho x,y,z thoã mãn (z-1)x-y=1 và x+2y=2
Chứng minh rằng \(\left(2x-y\right)\left(z^2-z+1\right)\)=7 tìm tất cả các số nguyên thoã mãn phương trình trên
Tìm x, y nguyên thoã mãn
/3x+2/+/y-4/=10
Đặt: \(3x+2=a\)
\(y-4=b\)
Ta thấy: Để x nguyên thì \(a-2\) phải chia hết cho 3.
Những số nhỏ hơn 10 chia hết cho 3 là: \(3;6;9\)
Vậy \(a\in\left\{5;-1;-4;-7;8;11\right\}\) mà \(11>10\Rightarrow a\in\left\{5;8;-1;-4;-7\right\}\)
Xét \(a=5\Rightarrow3x=3\Rightarrow x=1\)
\(\Rightarrow b=5\Rightarrow y=9\)
\(b=-5\Rightarrow y=-1\)
Xét \(a=8\Rightarrow3x=6\Rightarrow x=2\)
\(\Rightarrow b=2\Rightarrow y=6\)
\(b=-2\Rightarrow y=2\)
Xét \(a=-1\Rightarrow3x=-3\Rightarrow x=-1\)
\(\Rightarrow b=9\Rightarrow y=13\)
\(b=-9\Rightarrow y=-5\)
Xét \(a=-4\Rightarrow3x=-6\Rightarrow x=-2\)
\(\Rightarrow b=8\Rightarrow y=12\)
\(b=-8\Rightarrow y=-4\)
Xét \(a=-7\Rightarrow3x=-9\Rightarrow x=-3\)
\(\Rightarrow b=3\Rightarrow y=7\)
\(b=-3\Rightarrow y=1\)
Kết luận: ......
Đúng 0
Bình luận (0)
Tìm các số nguyên dương x, y, z thoã mãn 3^x+2^y=1+2^z
Ta thấy [TEX]y \geq 1[/TEX].
+ Nếu [TEX]y=1[/TEX] thì ta có [TEX]3^x=2^z-1[/TEX].
Xét tính chia hết cho 3 dễ thấy [TEX]z \vdots 2[/TEX]. Đặt [TEX]z=2k (k \in \mathbb{N}^*)[/TEX]
Ta có: [TEX]3^x=2^{2k}-1=(2^k-1)(2^k+1)[/TEX]
Đặt [TEX]2^k-1=3^m, 2^k+1=3^n (m,n \in \mathbb{N}^*; m+n=z) [/TEX]
Ta có: [TEX]3^n-3^m=2 \Rightarrow n=1, m=1 \Rightarrow z=2[/TEX]
[TEX]\Rightarrow z=1[/TEX]. Từ đó ta có bộ [TEX](x,y,z)=(1,1,2)[/TEX]
+ Nếu [TEX]y \geq 2[/TEX] thì ta có [TEX]2^z-2^y=3^x-1 > 0 \Rightarrow z >y[/TEX]
Lại có: [TEX]z>y \geq 2 \Rightarrow 3^x-1 \vdots 4 \Rightarrow x \vdots 2[/TEX]
Khi đó nếu [TEX]y \geq 4[/TEX] thì [TEX]3^x-1 \vdots 16 \Rightarrow x \vdots 4[/TEX]
[TEX]x=4q\Rightarrow 2^z-2^y=81^q-1\equiv 0(\text{mod 5})\Rightarrow 2^z-2^y\vdots 5\Rightarrow 2^y(2^{z-y}-1)\vdots 5[/TEX]
Từ đó [TEX]2^{z-y}-1 \vdots 5 \Rightarrow z-y=4k+2 \Rightarrow z-y \vdots 2 \Rightarrow 2^{z-y}-1 \vdots 3[/TEX]
[TEX]\Rightarrow 3^x-1 \vdots 3[/TEX](mâu thuẫn)
Suy ra [TEX]2 \leq y \leq 3[/TEX].
Nếu [TEX]y=2[/TEX] thì [TEX]3^x+3 =2^z \vdots 3[/TEX](mâu thuẫn)
Nếu [TEX]y=3[/TEX] thì [TEX]3^x+7=2^z[/TEX]. Xét đồng dư với 3 nên [TEX]z \vdots 2[/TEX].
Đặt [TEX]x=2m,z=2n \Rightarrow 2^{2n}-3^{2m}=7 \Rightarrow (2^n-3^m)(2^n+3^m)=7[/TEX]
[TEX]\Rightarrow 2^n-3^m=1,2^n+3^m=7 \Rightarrow n=2,m=1 \Rightarrow x=2,z=4[/TEX]
Vậy [TEX](x,y,z)=(1,1,2)[/TEX] hoặc [TEX](x,y,z)=(2,3,4)[/TEX]
Đúng 0
Bình luận (0)
tìm x,y thuộc N thoã mãn
2x + 1 = y2
Tìm các số x,y,z thoã mãn điều kiện. x+y+z=2√x-1 +4√2y-2 +6√z-3
Tìm x,y nguyên thoã mãn : x2 + xy + y2 = x2y2
mình làm thế này các bạn xem có đúng ko. nếu đúng thì k nhé
=> x2 + 2xy + y2 = x2y2 + xy
<=> (x+y)2 = (xy + 1/2$$)2 - 1/4$$
<=> (2x+2y)2 = (2xy + 1)2 - 1
<=> (2xy + 1)2 - (2x+ 2y)2 = 1
<=> (2xy + 1+ 2x+2y).(2xy + 1 - 2x- 2y) = 1 = 1.1 = (-1).(-1)
x; y nguyên nên ta có 2 trường hợp:
TH1: 2xy + 2x+ 2y + 1 = 1 và 2xy - 2x - 2y + 1 = 1
=> xy + x + y = 0 và 2xy + 2x+ 2y + 1 + 2xy - 2x - 2y + 1 = 2
=> xy + x + y = 0 và xy = 0
=> x + y = 0 và xy = 0 => x = y = 0
Th2: tương tự
Đúng 0
Bình luận (0)
x2 + xy + y2 = x2.y2
=> x2 + 2xy + y2 = ( x. y )2 + xy
=> ( x + y )2 = xy .( xy + 1 )
=> xy . ( xy + 1 ) là số chính phương
mà ( xy,xy + 1 ) = 1 , xy < xy + 1
=> xy = xy + 1 => vô lí
hoặc xy = 0 => xy . ( xy + 1 ) = 0 = 0 2 => x + y = 0= x y => x = y = 0
Vậy x = 0 ; y = 0
Đúng 0
Bình luận (0)
tìm x,y thuộc z thoã mãn 2xy-x+y=3
Tìm cặp số nguyên (x;y) thoã mãn:
|x+4|+|y-2|=3
Vì \(\left|x+4\right|\ge0;\left|y-3\right|\ge0\)
mà |x+4| + |y-3| =3 và |x+4| ; |y-3| thuộc Z
\(\Rightarrow\left(\left|x+4\right|;\left|y-3\right|\right)\in\left\{\left(0;3\right)\left(1;2\right)\left(3;0\right)\left(2;1\right)\right\}\)
Tương ứng \(\left(x;y\right)\in\left\{\left(-4;6\right);\left(-3;5\right);\left(-1;3\right);\left(-2;4\right)\right\}\)
Vậy \(\left(x;y\right)\in\left\{\left(-4;6\right);\left(-3;5\right);\left(-1;3\right);\left(-2;4\right)\right\}\)
Đúng 0
Bình luận (0)