Định lý 1

Trong một tam giác, góc đối diện với cạnh lớn hơn thi lớn hơn

Định lý 2

Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Định lý 1: Trong một tam giác, góc đối diện với cạnh lớn hơn thi lớn hơn

Định lý 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

-Nếu hai tam giác có hai cặp cạnh bằng nhau nhưng cặp cạnh thứ ba không bằng nhau thì góc đối diện với cạnh lớn hơn là góc lớn hơn.

-Ngược lại, nếu hai tam giác có hai cặp cạnh bằng nhau nhưng hai góc xen giữa không bằng nhau thì cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Trả lời

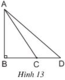
Trong tam giác ACD có góc ACD là góc tù .

Mà AD là cạnh đối diện với góc ACD.

⇒ AD là cạnh lớn nhất trong tam giác ACD (cạnh đối diện với góc tù là cạnh lớn nhất trong tam giác).

nên AD > AC hay AC < AD

Vậy Nếu : BC < BD thì AC < AD.

Nếu :  ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;

AM ≤ AC

+ Nếu M  ≡ A hoặc M  ≡  B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.

+ Nếu M nằm giữa B và C; ( M ≢  B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC

+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC

+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH

Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA

Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC

Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤  AB, AM ≤ AC

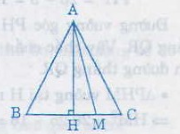
Giả sử   ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;

AM ≤ AC

+ Nếu M  ≡ A hoặc M  ≡  B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.

+ Nếu M nằm giữa B và C; ( M ≢  B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC

+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC

+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH

Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA

Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC

Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤  AB, AM ≤  AC

HÔM NAY, MÌNH VỪA HOÀN THIỆN XONG CÁI TOOL HACK FREE FREE. AI QUAN TÂM THÌ MÌNH SHARE CHO LINK TẢI TOOL NÈ: 
https://bom.to/rHvUS0