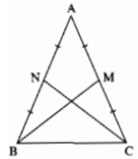
cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB.
a) chứng minh BM= CN
b) gọi O là trung điểm của BM và CN.
chứng minh tam giác BOC cân.
Cho tam giác ABC cân tại A. Gọi M, N thứ tự là trung điểm của AC và AB. gọi G là giao điểm của BM và CN. Chứng minh: a) tam giác AMN cân, b) BM = CN, c) tam giác GBC cân
a, Do \(NA=NB=\frac{1}{2}AB\)
\(AM=MC=\frac{1}{2}AC\)
Mà \(AB=AC\)\(\Rightarrow NA=MA;NB=MC\)\(\Rightarrow\)\(\Delta AMN\)cân tại \(A\)
b, Xét \(\Delta ANC\)và \(\Delta AMB\)có:
\(\widehat{BAC}chung\)
\(AB=AC\)
\(AN=AM\)(câu a)
\(\Rightarrow\Delta ANC=\Delta AMB\)
\(\Rightarrow BM=CN\)
c, Xét \(\Delta NBC\) và\(\Delta MCB\) có:
\(BCchung\)
NB = MC ( câu a)
NC = MB ( câu b)
=>\(\Delta NBC=\Delta MCB\)=>\(\widehat{GBC}=\widehat{GCB}\)=>\(\Delta GBC\) cân tại C
TYM cho chị nhé <3
Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB. Chứng minh rằng BM = CN
+) Do M là trung điểm của AC nên: 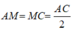 (1)
(1)
+) Do N là trung điểm của AB nên: 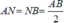 (2)
(2)
Lại có: AB = AC ( vì tam giác ABC cân tại A). (3)
Từ (1); (2); (3) suy ra: AN = NB = AM = MC.
+) Xét ∆ AMB và ∆ANC có:
Góc A chung
AM = AN ( chứng minh trên)
AB = AC ( vì tam giác ABC cân tại A)
Suy ra: ∆ AMB = ∆ANC ( c.g.c)
Do đó: BM = CN ( hai cạnh tương ứng).
Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB. Chứng minh BM = CN
Xét tam giác ABM và ACN
A la goc chung
AB=AC
AN=AM( deu la trung diem cua 2 canh bang nhau
=>Tam giac ABM=ACN=> BM=CN(dpcm)
xét tam giác ABM và ACN
A là góc chung
AB = AC
AN = AM ( đều là trung điểm của hai cạnh bằng nhau
= > Tam giác ABM=ACN=> BM= CN
chào em là thuthao ,em có một câu hỏi , em mới học lớp năm
Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB. Chứng minh rằng BM = CN ?
Ta có hình vẽ:
Theo bài ra ta có:
Tam giác ABC cân tại A
=> AB=AC ( hai cạnh bên của tam giác cân )
Ta lại có:
M là trung điểm của AC;N là trung điểm của AB
=> AN=BN=CM=AM
Ta có: \(\Delta ABM=\Delta ACN\) (c.g.c)
=> BM=CN ( hai cạnh tuơng ứng )
(đ.p.c.m)
Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB. Chứng minh rằng BM=CN
\(\hept{\begin{cases}AB=AC\\AM=\frac{1}{2}AC\\AN=\frac{1}{2}AB\end{cases}}\)
Từ đó suy ra AM=AN
=>BM=CN
ta có tam giác ABC cân tại A => AB=AC ( hai cạnh bên)
mà ta có AM =MC (vì m là trung điểm) => mc=\(\frac{1}{2}ac\)
ta lại có an =nb (vì n là trung điểm ab)=> nb=\(\frac{1}{2}ab\) mà ab=ac=> 1/2 ab=1/2ac hay mc=bn
xét tam giác bnc và tam giác cmb có:
bn=mc(cmt)
góc nbc=góc mcb
bc chung
do đó tam giác bnc = tam giác cmb (c.g.c)
=>nc=bm (hai cạnh tương ứng)
thông cảm hình vẽ quá xấu mình chắc chắn đúng đó
Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB. Chứng minh rằng BM = CN.
cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm của AC, AB
a) Chứng minh BM = CN và tam giác ABM = tam giác ACN
b) Gọi I là giao điểm của BM và CN. Chứng minh tam giác IBC cân
c) Chứng minh AI là tia phân giác của góc A
MÌNH TICK CHO BẠN NÀO NHANH VÀ ĐÚNG NHẤT NHA
a)
ta có: AB=AC suy ra 1/2 AB=1/2AC suy ra AN=NB=AM=MC
xét tam giác ABM và tam giác ACN có:
AB=AC
AM=AN(cmt)
A(chung)
suy ra tam giác ABM=ACN(c.g.c)
suy ra BM=CN
b)
ta có: I là trọng tâm cua tam giác ABC
ta có: MB=NC(theo câu a) suy ra 2/3MB=2/3NC suy ra IB=IC suy ra tam giac IBC cân tại I
c)
xét tam giác AIB và tam giác AIC có:
AB=AC
AI(chung)
IB=IC
suy ra tam giác AIB=AIC(c.c.c)
suy ra BAI=CAI
suy ra AI là phân giác của góc A
Cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm của AC và AB.
a) Chứng minh BM = CN và góc ABM = góc ACN.
b) Gọi I là giao điểm của BM và CN. Chứng minh tam giác IBC cân.
c) Chứng minh AI là phân giác của góc A.
d) Chứng minh AI vuông góc BC
CM BNC=CMB
MC=BN ; \(\widehat{B}=\widehat{C}\) ; BC chung
\(\Rightarrow\)BM=CN
CM ABM=ACN
AB=AC ; AM=AN ; \(\widehat{A}\) chung
\(\Rightarrow\)ABM =ACN \(\Rightarrow\) \(\widehat{ABM}=\widehat{ACN}\)
b \(\widehat{ABM}=\widehat{ACN}\) \(\Rightarrow\)\(\widehat{ABI}=\widehat{ACI}\);
\(\Rightarrow\) \(\widehat{AMB}=\widehat{ANC}\)\(\Rightarrow\)\(\widehat{BMC}=\widehat{CNB}\)
Xét BIN vs CIM : BN=CM ; \(\widehat{ACM}=\widehat{ACN};\)\(\widehat{BMC}=\widehat{CNB}\)
\(\Rightarrow\) IB=IC \(\Rightarrow\)IBC cân
c, Xét AIB và AIC : IB =IC ; \(\widehat{ABI}=\widehat{ACI};AB=AC\)
\(\Rightarrow\) \(\widehat{BAI}=\widehat{CAI}\)\(\Rightarrow\)AI pg góc A
d, xét BAD và CAD
góc BAI = CAI ; AB=AC ; AD chung
\(\Rightarrow\)góc ADB = ADC mà chúng cộng nhau = 180 \(\Rightarrow\)\(\widehat{D}\)= 90
Bài 2: Cho tam giác ABC cân tại A. Gọi M,N lần lượt là trung điểm của AC, AB.
a. Chứng minh BM=CN và ··ABM = ACN?
b. Gọi I là giao điểm của BM và CN. Chứng minh tam giác IBC cân?
c. Chứng minh AI là phân giác của góc A?
d. Chứng minh AI vuông góc với BC?
a/ Có AB = AC ( tam giácABC cân tại A) , mà M , N lan luot la trung điểm cua AC , AB Suy ra AM = AN Xét tam giác AMB và tam giác ANC có: Góc A : góc chung AB = AC ( tam giác ABC cân tại A) AM = AN ( cmt) Suy ra : tam giácAMB = tam giác ANC ( c - g - c) Suy ra BM = CN ( 2 cạnh t/ứng ) Phan b , c ,d mik đều làm đc nhunh giờ điện thoại mik hết pin rồi
Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB. Chứng minh rằng BM=CN