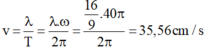cho 2 nguồn A và B cách nhau một khoảng 53(cm) có phương trình dao động uA=uB=6cos(80πt-π/2)(mm).Điểm D cách A 35 cm thuộc cực tiểu thứ 2 .Xác định khoảng cách từ D đến B.
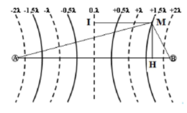
Trên mặt chất lỏng có hai nguồn kết hợp A, B cách nhau 10 cm dao động với phương trình u A = 4 cos ( 20 πt ) cm; u B = 5 cos ( 20 πt + π ) cm; tốc độ truyền sóng trên mặt chất lỏng là 20 cm/s. M là một điểm trên đường cực đại thứ 2 kể từ đường trung trực của AB và cách AB đoạn 4 cm. Tìm khoảng cách từ M đến trung trực của AB.
A. 5 cm.
B. 4 cm.
C. 3 cm.
D. 2 cm.
Chọn D
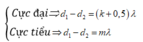
Cực tiêu thứ 2:
![]()
Giả sử MA – MB = 3 cm, hay
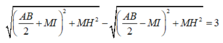
![]()
Ở bề mặt một chất lỏng có hai nguồn phát sóng kết hợp A và B cách nhau 20 cm. Hai nguồn này dao động theo phương thẳng đứng có phương trình lần lượt là u A = 5 cos ( 40 πt ) mm và u B = 5 cos ( 40 πt + π ) mm . Tốc độ truyền sóng trên mặt chất lỏng là 70 cm/s. Số điểm dao động với biên độ cực tiểu trên đoạn thẳng AB là:
A. 8.
B. 9.
C. 11.
D. 10.
Chọn C
+ Bước sóng của sóng λ = v 2 π ω = 3 , 5 c m
Số cực tiểu giao thoa trên đoạn thẳng nối hai nguồn ngược pha:
- A B λ ≤ k ≤ A B λ ⇔ - 5 , 7 ≤ k ≤ 5 , 7
Vậy có 11 điểm
Ở bề mặt một chất lỏng có hai nguồn phát sóng kết hợp A và B cách nhau 20 cm. Hai nguồn này dao động theo phương thẳng đứng có phương trình lần lượt là: u A = 5 cos ( 40 π t ) mm và u B = 5 cos ( 40 π t + π ) mm. Tốc độ truyền sóng trên mặt chất lỏng là 70 cm/s. Số điểm dao động với biên độ cực tiểu trên đoạn thẳng AB là:
A. 8
B. 9
C. 11
D. 10
- Bước sóng của sóng:
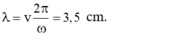
- Số cực tiểu giao thoa trên đoạn thẳng nối hai nguồn ngược pha:
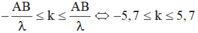
- Vậy có 11 điểm
Tại hai điểm A, B cách nhau 13 cm trên mặt nước có hai nguồn phát sóng giống nhau. Cùng dao động theo phương trình u A = u B = acosωt cm. Sóng truyền đi trên mặt nước có bước sóng là 2 cm, coi biên độ sóng không đổi khi truyền đi. Xét điểm M trên mặt nước thuộc đường thằng By vuông góc với AB và cách A một khoảng 20 cm. Trên By, điểm dao động với biên độ cực đại cách M một khoảng nhỏ nhất bằng:
A. 2,33 cm.
B. 4,11 cm.
C. 3,14 cm.
D. 2,93 cm.
Đáp án B
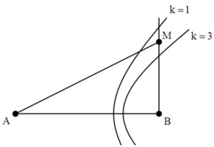
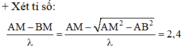
Vậy để N là một cực đại trên By và gần M nhất thì N chỉ có thể thuộc hypebol ứng với k = 3 hoặc k = 1.
+ Với k = 1, ta có:

Tại mặt chất lỏng có hai nguồn phát sóng kết hợp A, B cách nhau 16 cm, dao động điều hòa theo phương vuông góc với mặt chất lỏng với phương trình u A = 2 cos 40 πt cm và u B = 2 cos 40 πt + π cm. Tốc độ truyền sóng trên mặt chất lỏng là 40 cm/s. Gọi M là một điểm thuộc mặt chất lỏng, nằm trên đường thẳng Ax vuông góc với AB, cách A một đoạn ngắn nhất mà phần tử chất lỏng tại M dao động với biên độ cực đại. Khoảng cách AM bằng:
A. 1,42 cm
B. 2,14 cm
C. 2,07 cm
D. 1,03 cm
Tại mặt chất lỏng có hai nguồn phát sóng kết hợp A, B cách nhau 16 cm, dao động điều hòa theo phương vuông góc với mặt chất lỏng với phương trình u A = 2 cos 40 π t c m và u B = 2 cos 40 π t + π c m . Tốc độ truyền sóng trên mặt chất lỏng là 40 cm/s. Gọi M là một điểm thuộc mặt chất lỏng, nằm trên đường thẳng Ax vuông góc với AB, cách A một đoạn ngắn nhất mà phần tử chất lỏng tại M dao động với biên độ cực đại. Khoảng cách AM bằng:
A. 1,42 cm
B. 2,14 cm
C. 2,07 cm
D. 1,03 cm
Đáp án D
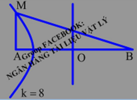
Bước sóng: λ = v f = 40 20 = 2 c m
Vì hai nguồn ngược pha nên điều kiện cực đại cho M là: M A − M B = k + 0 , 5 λ = 2 k + 1
Vì M gần A nhất nên M phải thuộc cực đại ngoài cùng về phía A.
Số cực đại trên AB: − A B λ − 1 2 < k < A B λ − 1 2
⇒ − 8 , 5 < k < 8 , 5 ⇒ k = − 8 ⇒ M A − M B = 2 − 8 + 1 = − 15 ⇒ M B = M A + 15 1
Vì Δ A M B vuông tại A nên: M A 2 + A B 2 = M B 2 2
Thay (1) vào (2) ta có: M A 2 + 16 2 = M A + 15 2 ⇒ M A = 1 , 03 c m
Tại mặt chất lỏng có hai nguồn phát sóng kết hợp A, B cách nhau 16 cm, dao động điều hòa theo phương vuông góc với mặt chất lỏng với phương trình u A = 2 cos 40 π t cm và u B = 2 cos 40 π t + π cm. Tốc độ truyền sóng trên mặt chất lỏng là 40 cm/s. Gọi M là một điểm thuộc mặt chất lỏng, nằm trên đường thẳng Ax vuông góc với AB, cách A một đoạn ngắn nhất mà phần tử chất lỏng tại M dao động với biên độ cực đại. Khoảng cách AM bằng:
A. 1,42 cm
B. 2,14 cm
C. 2,07 cm
D. 1,03 cm
Đáp án D
+ Bước sóng: λ = v f = 40 20 = 2 c m
+ Vì hai nguồn ngược pha nên điều kiện cực đại cho M là: M A − M B = k + 0 , 5 λ = 2 k + 1
+ Vì M gần A nhất nên M phải thuộc cực đại ngoài cùng về phía A.
+ Số cực đại trên AB: − A B λ − 1 2 < k < A B λ − 1 2
⇒ − 8 , 5 < k < 8 , 5 ⇒ k = − 8
⇒ M A − M B = 2 − 8 + 1 = − 15 ⇒ M B = M A + 15 1
+ Vì Δ A M B vuông tại A nên: M A 2 + A B 2 = M B 2 2
+ Thay (1) vào (2) ta có: M A 2 + 16 2 = M A + 15 2 ⇒ M A = 1 , 03 c m
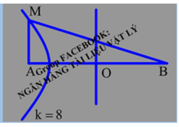
2 nguồn sóng A và B kết hợp cách nhau 12cm dao dộng teo phương trình uA=a1cos(20pi.t)cm vào uB=a2cos(20pi.t+pi/2) .tốc độ truyền sóng là 20cm/s . Điểm dao động với biên độ cực tiểu trên AB cách trung điểm O của AB một khoảng lớn nhất bằng bao nhiêu .
Hai nguồn vuông pha sẽ không có trong đề thi đâu bạn nhé
Bước sóng \(\lambda = v/f=2cm\)
Lấy B' cách B \(\dfrac{\lambda}{4}\), khi đó B' trễ pha \(\pi/2\) so với B \(\Rightarrow\) B' cùng pha với A.
Điểm M dao động biên độ cực tiểu khi
\(MB'-MA=(k+0,5)\lambda\)
\(\Rightarrow d_2-\dfrac{\lambda}{4}-d_1=(k+0,5)\lambda\)
\(\Rightarrow d_2-d_1=(k+0,75)\lambda\)
\(-12\le d_2-d_1\le12\)
\(\Rightarrow -12\le (k+0,75).2\le12\)
\(\Rightarrow -6,74\le k \le5,25\)
Bạn xét k = -6 hoặc k = 5 để tìm \(d_1, d_2\), lấy giá trị d nhỏ nhất, từ đó suy ra khoảng cách lớn nhất.
Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 20 cm, dao động theo phương thẳng đứng với phương trình u A = a 1 cos ( 40 π t + π / 3 ) và u B = a 2 cos ( 40 π t – π / 6 ) (uA và uB tính bằng cm, t tính bằng s). Dao động của phần tử vật chất tại M cách A và B lần lượt 12 cm và 16 cm có biên độ cực tiểu. Biết giữa M và đường trung trực còn có hai dãy cực đại khác. Tốc độ truyền sóng trên mặt chất lỏng là:
A. 35,56 cm/s
B. 29,09 cm/s
C. 45,71 cm/s
D. 60,32 cm/s
- Từ phương trình của 2 nguồn ta thấy sóng của 2 nguồn vuông pha nhau thì số cực đại và cực tiểu là như nhau và:
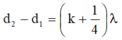
- Giữa M và đường trung trực AB còn có 2 dãy cực đại và tại M là cực tiểu → k = 2
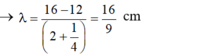
- Tốc độ truyền sóng là: