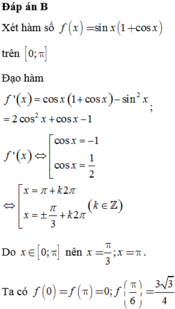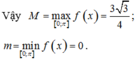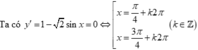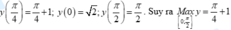giá trị nhỏ nhất của hàm số y−x+cosx trên [0;frac{pi}{2}] là bao nhiêu ?
Đọc tiếp
giá trị nhỏ nhất của hàm số y=−x+cosx trên [0;\(\frac{\pi}{2}\)] là bao nhiêu ?
Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của hàm số: y
1
2
-
cosx
+
1
1
+
cosx
với
x
∈
0
;
π
2
A. 2 B.
2
3
C.
4...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số: y = 1 2 - cosx + 1 1 + cosx với x ∈ 0 ; π 2
A. 2
B. 2 3
C. 4 3
D. Tất cả sai
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) sinx (1+cosx) trên đoạn
0
;
π
A.
M
3
3
2
;
m
1
B.
M
3
3
4
;
m
0
C. ...
Đọc tiếp
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = sinx (1+cosx) trên đoạn 0 ; π
A. M = 3 3 2 ; m = 1
B. M = 3 3 4 ; m = 0
C. M = 3 3 ; m = 1
D. M = 3 ; m = 1
Tìm giá trị nhỏ nhất của hàm số
y
cos
x
+
cos
x
-
2
π
3
trên R A.
m
i
n
R
y
2
B.
m
i
n...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = cos x + cos x - 2 π 3 trên R
A. m i n R y = 2
B. m i n R y = 1
C. m i n R y = - 2
D. m i n R y = - 1
Tìm giá trị nhỏ nhất của hàm số
y
cos
x
+
cos
(
x
-
2
π
3
)
trên R A. B. C. D.
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = cos x + cos ( x - 2 π 3 ) trên R
A. 
B. 
C. 
D. 
Cho hàm số
f
x
liên tục, không âm trên đoạn
0
;
π
2
, thỏa mãn
f
0
3
và
f...
Đọc tiếp
Cho hàm số f x liên tục, không âm trên đoạn 0 ; π 2 , thỏa mãn f 0 = 3 và f x . f ' x = cos x . 1 + f 2 x , ∀ x ∈ 0 ; π 2 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số f x trên đoạn π 6 ; π 2 .
A. m = 21 2 , M = 2 2 .
B. m = 5 2 , M = 3
C. m = 5 2 , M = 3 .
D. m = 3 , M = 2 2 .
Cho hàm số
f
x
liên tục, không âm trên đoạn
0
;
π
2
thỏa mãn
f
0
3
và
f
x
....
Đọc tiếp
Cho hàm số f x liên tục, không âm trên đoạn 0 ; π 2 thỏa mãn f 0 = 3 và f x . f ' x = cos x . 1 + f 2 x , ∀ x ∈ 0 ; π 2 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số f x trên đoạn π 6 ; π 2
A. m = 21 2 , M = 2 2
B. m = 5 2 , M = 3
C. m = 5 2 , M = 3
D. m = 3 , M = 2 2
Chọn đáp án A
Từ giả thiết
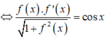
Suy ra
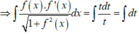
Từ (1) và (2) suy ra 1 + f 2 x = sin x + C
Thay x = 0 vào ta được:
do f 0 = 3
Suy ra
do hàm số f x liên tục, không âm trên 0 ; π 2
Đặt t = sin x
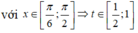
Xét hàm số g t = t 2 + 4 t + 3 trên 1 2 ; 1
Ta có
⇒ Hàm số g t đồng biến trên 1 2 ; 1
Khi đó
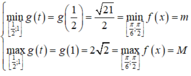
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của hàm số
y
x
+
2
.
cos
x
trên
0
,
π
2
A
.
2
B...
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y = x + 2 . cos x trên 0 , π 2
A . 2
B . 3
C . π 4 + 1
D . π 2
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
f
x
sin
x
1
+
cos
x
trên đoạn
0
;
π
A.
M
3
3
2
;
m
1
B.
M...
Đọc tiếp
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f x = sin x 1 + cos x trên đoạn 0 ; π
A. M = 3 3 2 ; m = 1
B. M = 3 3 4 ; m = 0
C. M = 3 3 ; m = 1
D. M = 3 ; m = 1
Đáp án B
Cách 1: Tư duy tự luận
Xét hàm số f x = sin x 1 + cos x trên 0 ; π
Đạo hàm f ' x = cos x 1 + cos x − sin 2 x = 2 cos 2 x + cos x − 1 ;
f ' x ⇔ cos x = − 1 cos x = 1 2 ⇔ x = π + k 2 π x = ± π 3 + k 2 π k ∈ ℤ
Do x ∈ 0 ; π nên x = π 3 ; x = π .
Ta có
f 0 = f π = 0 ; f π 6 = 3 3 4
Vậy
M = max 0 ; π f x = 3 3 4 ; m = min 0 ; π f x = 0
Cách 2: Sử dụng máy tính cầm tay
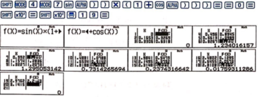
Quan sát bảng giá trị, ta thấy
M = max 0 ; π f x ≈ 1,295... ≈ 3 3 4 ; m = min 0 ; π f x = 0
Đúng 0
Bình luận (0)
Cho hàm số f(x) cos2x - cosx + 1. Giá trị nhỏ nhất của hàm số trên
ℝ
là A.
-
1
8
B.
-
1
4
C.
1
9
D. 1
Đọc tiếp
Cho hàm số f(x) = cos2x - cosx + 1. Giá trị nhỏ nhất của hàm số trên ℝ là
A. - 1 8
B. - 1 4
C. 1 9
D. 1
Giá trị nhỏ nhất của hàm số sau trên khoảng (0;
π
/2) là:
y
1
sinx
+
cosx
A. 1 B. 2
2
C. -
2
D.
2
/2
Đọc tiếp
Giá trị nhỏ nhất của hàm số sau trên khoảng (0; π /2) là:
y = 1 sinx + cosx
A. 1 B. 2 2
C. - 2 D. 2 /2
Đáp án: D.
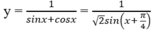
Trên khoảng (0; π /2), sin(x + π /4) ≤ 1;
Dấu "=" xảy ra ⇔ x = π /4
Suy ra giá trị nhỏ nhất của hàm số là min y = y( π /4) = 2 /2.
Đúng 0
Bình luận (0)