cho tam giac abc đều có độ dài cạnh là a ;Tính đường cao va diện tích của tam giac do

Những câu hỏi liên quan
cho tam giac abc vuông tại a, i là điểm cách đều 3 cạnh của tam giác một đoạn bằng R. Biết ab có độ dài bằng c, BC có độ dài bằng c, AC=b. CMR r=1/2(b+c-a)
Có lời giải nha
cho tam giác abc có tổng độ dài cạnh AB va BC la 91cm. Tổng độ dài của cạnh BC và AC là 105cm ; tổng độ dài của cạnh AC và AB là 124cm.Cac canh cua hinh tam giac dai bao nhieu dm
chu vi HTG : (91+105+124):2=160
Độ dài cạnh AB là : 160 - 105 = 55
Độ dài cạnh AC là : 124 - 55 = 69
Độ dài cạnh BC là : 91 - 55 = 36
sorry , mk thíu : 55cm = 5,5dm
69cm=6,9dm
36cm=3,6dm
Cho hình tam giac ABC có cạnh BC = 10 cm.Gọi M là tung điểm cạnh AC.Tính độ dài cạnh MN
Cho hình tam giac ABC có cạnh BC = 10 cm.Gọi M là tung điểm cạnh AC.Tính độ dài cạnh MN
Cho hình tam giac ABC có cạnh BC = 10 cm.Gọi M là tung điểm cạnh AC.Tính độ dài cạnh MN
Đúng 0
Bình luận (0)
bạn đọc lại bài bạn ra mình thấy vẫn còn thiếu !
Đúng 0
Bình luận (0)
cho tam giác ABC có tổng độ dài cạnh thứ nhất và cạnh thứ hai là 18,25cm,tổng độ dài cạnh thứ hai và cạnh thứ ba là 23,55cm,tổng độ dài cạnh thứ ba và cảnh thứ nhất là 20,3 cm.tinh chu vi hinh tam giac do
2 lần chu vi của ABC là:
18,25 + 23,55 + 20,3 = 62,1 (cm)
Chu vi của ABC là:
62,1 : 2 = 31,05 (cm)
Đ/S:...
Đúng 0
Bình luận (0)
2 lần chu vi của tam giác ABC là
18,25 + 23,55 + 20,3 = 62,1 ( cm )
Chu vi hình tam giác ABC là :
62,1 : 2 = 31,5 ( cm )
Đ/S : 31,5 cm
tk chó mk nhé
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
mot tam giac ABC vuong ở A và có chu vi là 120cm.Biết độ dài cạch AC bằng 75%độ dài cạnh AB.Đọ dai canh BC bằng 5/7 tổng độ dài hai cạnh ACva AB.Tính chieu caoAH ứng với cạnh BC của tam giác ABC?
Xem thêm câu trả lời
Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC}\)
Dựng hình bình hành ABDC.
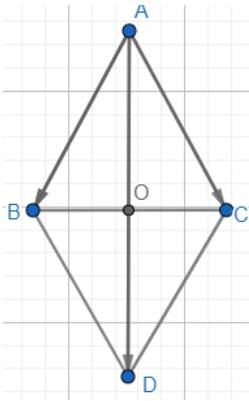
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)
Đúng 0
Bình luận (0)
Tam giac ABC có chu vi là 58 cm. Tổng độ dài cạnh AB và cạnh BC là 42cm, tổng độ dài cạnh BC và cạnh AC là 34cm. Tính độ dài các cạnh AB; AC; BC của tam giác
Độ dài của cạnh AC là: 58-42=16(cm)
Độ dài của cạnh AB là: 58-34=24(cm)
Độ dài của cạnh BC là: 34-16=18(cm)
please :3
ac=16cm,ab24cm,bc18cm
Cho tam giác đều ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC.
Các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC là:
\(\overrightarrow {AB} ;\;\overrightarrow {BA} ;\;\overrightarrow {AC} ;\;\overrightarrow {CA} ;\;\overrightarrow {BC} ;\;\overrightarrow {CB} \)
Chú ý khi giải:
Vectơ \(\overrightarrow {AB} \) khác vectơ \(\overrightarrow {BA} \) (khác nhau điểm đầu và điểm cuối).
Đúng 0
Bình luận (0)



















