Tính diện tích của tam giác ABC , góc A = 90 dộ , AB = 6cm , BC = 10cm

Những câu hỏi liên quan
Cho tam giác ABC có góc A bằng 90 độ,AB=6cm,BC=10cm,đường phân giác BM(M thuộc AC).Từ A hạ AH vuông góc BM cắt BC tại điểm K a)Chứng minh: tam giác AMB đồng dạng với tam giác HKB b)Tính AC,AM,BM c)Tính diện tích tam giác BHK d)Chứng minh: AK.BK bằng 2AM.BH
cho tam giác abc có ab=6cm,ac=8cm,bc=10cm. Kẻ ah vuông góc vs bc tại h 1 chứng minh tam giác abc vuông tại a 2 tính diện tích tam giác abc 3 tính AH
1) Ta có: \(BC^2=10^2=100\)
\(AB^2+AC^2=6^2+8^2=100\)
Do đó: \(BC^2=AB^2+AC^2\)(=100)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
2) Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
3) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm
Đúng 0
Bình luận (1)
Ta có: BC2=102=100
AB2+AC2=62+82=100
Vậy BC2=AB2+AC2
Xét ΔABC có:
BC2=AB2+AC2
Nên ΔABC vuông tại A(Định lí Pytago đảo)
Ta có: ΔABC vuông tại A(gt)
Nên
Đúng 1
Bình luận (0)
cho tam giác ABC có góc A=90 độ,bk AB=6cm,BC=10cm,AH vuông góc với BC
câu a.tính AC?
câu b.qua B kẻ đường thẳng vuông góc với AB cắt AH tại D.CHỨNG MINH tam giác ABC đồng dạng với tam giác BDA
câu c.tính diện tích tam giác ABC/tam giác BDA?
a) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\) \(AC^2=BC^2-AB^2\)
\(\Leftrightarrow\) \(AC^2=10^2-6^2=64\)
\(\Leftrightarrow\) \(AC=\sqrt{64}=8\)cm
b) Xét \(\Delta ABC\) và \(\Delta BDA\)có:
\(\widehat{BAC}=\widehat{DBA}=90^0\)
\(\widehat{ACB}=\widehat{BAD}\) (cùng phụ với góc DAC)
suy ra: \(\Delta ABC~\Delta BDA\)
c) \(\Delta ABC~\Delta BDA\)
\(\Rightarrow\)\(\frac{S_{ABC}}{S_{BDA}}=\left(\frac{AC}{AB}\right)^2=\left(\frac{8}{6}\right)^2=\left(\frac{4}{3}\right)^2=\frac{16}{9}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=6cm, AC=8cm, BC=10cm. Kẻ AH vuông góc với BC tại H
a, Tính diện tích tam giác ABC
b, Tính AH, BH, CH
a) Diện tích tam giác ABC (Heron)
\(S_{ABC}=\frac{1}{4}\sqrt{\left(AB+BC+AC\right)\left(AB+BC-AC\right)\left(BC+AC-AB\right)\left(AC+AB-BC\right)}\)
\(S_{ABC}=\frac{1}{4}\sqrt{\left(6+10+8\right)\left(6+10-8\right)\left(10+8-6\right)\left(8+6-10\right)}=24\left(cm^2\right)\)
b)Xét tam giác ABC có
\(BC^2=10^2=100\left(cm\right)\)
\(AB^2+AC^2=6^2+8^2=100\left(cm\right)\)
Vì 100cm=100cm
\(\Rightarrow BC^2=AB^2+AC^2\)
=> Tam giác ABC vuông tại A
Xét diện tích tam giác ABC thường \(S_{ABCt}=\frac{AH.BC}{2}\left(1\right)\)
Xét diện tích tam giác ABC vuông \(S_{ABCv}=\frac{AC.AB}{2}\left(2\right)\)
Từ (1) và (2)
\(\Leftrightarrow AH.BC=AB.AC\)
\(\Leftrightarrow AH.10=8.6\Leftrightarrow AH=4,8\left(cm\right)\)
Xét tam giác ABH vuông tại H
\(\Rightarrow BH^2=AB^2-AH^2\left(PYTAGO\right)\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}\)
\(\Rightarrow BH=\sqrt{6^2-13,3^2}=3,6\left(cm\right)\)
Xét tam giác ACH vuông tại H
\(\Rightarrow HC^2=AC^2-AH^2\left(PYTAGO\right)\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}\)
\(\Rightarrow HC=\sqrt{8^2-4,8^2}=6,4\left(cm\right)\)
bút chì đọc tiếng anh là gì ?
1+1=????
ôppopopoppoo
Cho tam giác ABC có Â= 90° ; AB = 6cm; BC = 10cm. a) Tính AC. b) Kẻ AH vuông góc với BC. Tính AH.
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{100-36}=\sqrt{64}=8cm\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AB.AC\)
\(\Rightarrow AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=\dfrac{24}{5}=4,8cm\)
Đúng 2
Bình luận (0)
a, Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=\sqrt{100-36}=8cm\)
b, Xét tam giác ABH và tam giác CBA có :
^B _ chung
^BAH = ^BCA ( cùng phụ ^HAC )
Vậy tam giác ABH ~ tam giác CBA ( g.g )
=> AH/AC = AB/BC => AH = 6.8:10 = 4,8 cm
Đúng 1
Bình luận (0)
cho tam giác ABC vuông A có AB=6cm, BC=10cm, đường phân giác BD Kẻ DH vuông góc BC
1, tính tỉ số đường cao AD/CD
2, Cm AB. DC=HD.BC
3, Tính diện tích tam giác DHC
1: Xét ΔABC có BD là đường phân giác
nên AD/CD=AB/BC=3/5
2: Xét ΔCHD vuông tại H và ΔCAB vuông tại A có
\(\widehat{C}\) chung
do đó: ΔCHD∼ΔCAB
Suy ra: HD/AB=CD/CB
hay \(CD\cdot AB=HD\cdot CB\)
Đúng 0
Bình luận (0)
Bài 1:Tam giác ABC, góc A=90 độ, góc C=30 độ, AB=6cm, trung tuyến AM.Tính AM
Bài 2: Tam giác ABC cân tại A, AB=10cm, BC=6cm, trung tuyến AM, trọng tâm G. Tính GA, GM
Tam giác \(ABC\) có \(AB = 6cm,AC = 8cm,BC = 10cm\). Đường phân giác của góc \(BAC\) cắt cạnh \(BC\) tại \(D\).
a) Tính độ dài các đoạn thẳng \(DB\) và \(DC\).
b) Tính tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\).
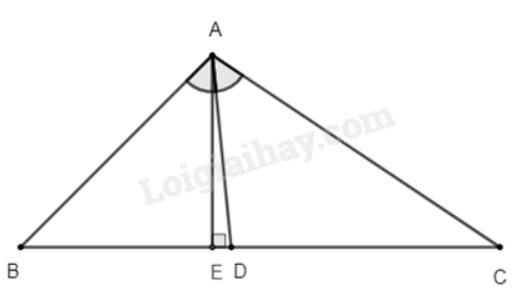
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 10 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{10 - BD}} = \frac{6}{8} \Leftrightarrow 8BD = 6.\left( {10 - BD} \right) \Rightarrow 8BD = 60 - 6BD\)
\( \Leftrightarrow 8BD + 6BD = 60 \Leftrightarrow 14BD = 60 \Rightarrow BD = \frac{{60}}{{14}} = \frac{{30}}{7}\)
\( \Rightarrow DC = 10 - \frac{{30}}{7} = \frac{{40}}{7}\)
Vậy \(BD = \frac{{30}}{7}cm;DC = \frac{{40}}{7}cm\).
b) Kẻ \(AE \bot BC \Rightarrow AE\) là đường cao của tam giác \(ABC\).
Vì \(AE \bot BC \Rightarrow AE \bot BD \Rightarrow AE\)là đường cao của tam giác \(ADB\)
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = \frac{1}{2}BD.AE\)
Vì \(AE \bot BC \Rightarrow AE \bot DC \Rightarrow AE\)là đường cao của tam giác \(ADC\)
Diện tích tam giác \(ADC\) là:
\({S_{ADC}} = \frac{1}{2}DC.AE\)
Ta có: \(\frac{{{S_{ADB}}}}{{{S_{ADC}}}} = \frac{{\frac{1}{2}AE.BD}}{{\frac{1}{2}AE.CD}} = \frac{{BD}}{{DC}} = \frac{{\frac{{30}}{7}}}{{\frac{{40}}{7}}} = \frac{3}{4}\).
Vậy tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\) là \(\frac{3}{4}\).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. M là trung điểm của BC. Kẻ MD vuông góc AB, ME vuông góc với AC. 1, Tứ giác ADME, BDME, DMCE là hình gì ? 2, Cho AB = 6cm, BC = 10cm, Tính diện tích ADME 3,Kẻ AH vuông góc BC. Chứng minh tứ giác DHME là hình thang cân 4,Kẻ đường thẳng song song với DH qua A, cắt DE tại N. Chứng minh ADHN là hình bình hành
1: Xét tứ giác ADME co
góc ADM=góc AEM=góc DAE=90 độ
nên ADME là hình chữ nhật
Xét ΔABC có
DM//AC
nên DM/AC=BD/BA=BM/BC
=>D là trung điểm của BA
Xét ΔABC có ME//AB
nên ME/AB=CM/CB=CE/CA=1/2
=>E là trung điểm của AC
=>EM//BD và EM=BD
=>BMED là hình bình hành
Xét tứ giác DMCE có
DM//CE
DM=CE
Do đó: DMCE là hình bình hành
2: \(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
AD=AB/2=3cm
AE=AC/2=4cm
\(S_{ADME}=3\cdot4=12\left(cm^2\right)\)
3: ΔHAC vuông tại H
mà HE là trung tuyến
nên HE=AC/2=MD
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
Xét tứ giác DHME có
DE//MH
MD=HE
Do đo: DHME là hình thang cân
Đúng 0
Bình luận (0)























