vẽ tam giác mnp biết MN=2,5 cm,NP=3cm, PM=5cm

Những câu hỏi liên quan
vẽ vào vở tam giác MNP biết MN=2,5 cm ;NP=3 cm;PM=5cm
b)vẽ vào vở tam giác EFG có EF=FG=GE=3cm sau đó đo ba góc của tam giác EFG rồi cho biết số đo của mỗi góc
Vẽ tam giác MNP biết MN = 2,5cm, NP = 3cm, PM = 5cm.
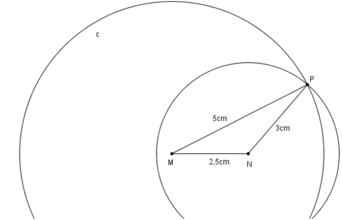
- Vẽ đoạn thẳng MN = 2,5cm.
- Trên cùng một nửa mặt phẳng bờ MN vẽ cung tròn tâm M bán kính 5cm, và cung tròn tâm N bán kính 3cm
- Hai cung tròn cắt nhau tại P. Vẽ các đoạn thẳng MP, NP ta được tam giác MNP.
Đúng 0
Bình luận (0)
Vẽ tam giác MNP biết MN = 2,5cm, NP = 3cm, PM = 4cm ?
-Vẽ đoạn MN= 2,5cm
- Trên cùng một nửa mặt phẳng bở MN vẽ cung trong tâm M bán kính 5cm và cung tròn tâm N bán kinh 5cm.
- Hai cung tròn cắt nhau tại P. Vẽ các đoạn MN, NP, ta được tam giác MNP.
Đúng 0
Bình luận (1)
Vẽ tam giác MPN biết MN=2,5cm,NP=3cm,PM=5cm
Bước 1: Vẽ cạnh NP nằm ngang bằng 3 cm.
Bước 2: Sử dụng com-pa với độ mở là 2,5 cm, vẽ đường tròn tâm N bán kình 2,5 cm.
Sử dụng com-pa với độ mở là 5 cm, vẽ đường tròn tâm P bán kính 5 cm.
Giao điểm của đường tròn tâm N bán kính 2,5 cm và đường tròn tâm P bán kính 5 cm chính là điểm M cần tìm.
Bước 3: Nối M với N, M với P, ta có tam giác MNP cần dựng.
Mình không vẽ bằng máy được nên hướng dẫn bạn cách vẽ, bạn thông cảm nhé!
Đúng 0
Bình luận (0)
bài 1: vẽ đoạn thẳng AB =6cm vẽ đường tròn tâm A bán kính 3cm ,vẽ đường tròn tâm B bán kính 4 cm.Đường tròn (A;3cm) cắt (B;4cm) tại C và D .Tính chu vi tam giác ACB và tam giác ADB ?
bài 2 Nêu cách vẽ tam giác MNP biết MN=5cm,NP=3m,PM=7cm
<help meeeeeee>thanks
Câu 6 : Vẽ tam giác MNP biết MN=3cm;MP=5cm;NP=4cm(Nói rõ cách vẽ).Lấy điểm nằm trong tam giác MNP, vẽ tia MA, đường thẳng NA và đoạn thẳng PA
Cho tam giác ABC có AB=3cm,BC=5cm,AC=6cm và tam giác MNP có MN=9cm,NP=4,5cm,PM=7,5cm.
CMR: tam giác ABC∼tam giác NPM
Giups mk vs ạ ai nhanh mk tick nha :>
Xét ΔABC và ΔNPM có
\(\dfrac{AB}{NP}=\dfrac{AC}{NM}=\dfrac{BC}{PM}\)
Do đó: ΔABC∼ΔNPM
Đúng 2
Bình luận (0)
Vẽ tam giác MNP biết MN=4cm,NP=5cm và PM=6cm
Cho tam giác MNP có MN=3cm MP= 4cm NP=5cm a, Chứng tỏ rằng tam giác MNP vuông tại M b, vẽ tia phân giác ND(D thuộc MP) từ D vẽ DE vuông góc với NP (E thuộc NP) chứng minh DM=DE c, ED cắt MN tại F chứng minh DE
a: NP^2=MN^2+MP^2
=>ΔMNP vuông tại M
b: Xét ΔNMD vuông tại M và ΔNED vuông tại E có
ND chung
góc MND=góc END
=>ΔNMD=ΔNED
=>DM=DE
Đúng 0
Bình luận (0)




















